题目内容
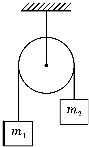如图所示，质量为m1；和m2：的两个物体，系在一条跨过光滑定滑轮的不一可伸长的轻绳两端．己知m1+m2=1kg，当m2改变时，轻绳的拉力也会不断变化．若轻绳所能承受的最大拉力为4.8N，为保证轻绳不断，试求m2的范围．（重力加速度g=l 0m/s2）分析：采用隔离法分别对两个物块进行受力分析列牛顿第二定律方程求出绳子上的拉力，然后即可求出物块的质量范围
解答：解：以 为研究对象m1，由牛顿第二定律：T-m1g=m1a
以m2 为研究对象，由牛顿第二定律：m2g-T=m2a
联立，得：T=
g
由题意T＜4.8N，且 m1+m2=1kg，代入可得：
m22-m1+0.24＞0
所以0＜m2＜0.4kg或1kg＞m2＞0.6kg
答：m2的范围是0＜m2＜0.4kg或1kg＞m2＞0.6kg．
以m2 为研究对象，由牛顿第二定律：m2g-T=m2a
联立，得：T=
| 2m1m2 |
| m1+m2 |
由题意T＜4.8N，且 m1+m2=1kg，代入可得：
m22-m1+0.24＞0
所以0＜m2＜0.4kg或1kg＞m2＞0.6kg
答：m2的范围是0＜m2＜0.4kg或1kg＞m2＞0.6kg．
点评：本题属于连接体问题，受力分析是关键．有时候也采用先整体后隔离的分析方法．
练习册系列答案
期末集结号系列答案
相关题目
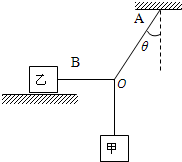如图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O．轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态．（已知：sin37°=0.6，cos37°=0.8）求：
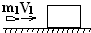如图所示，质量为m1=10g的子弹以800m/s的速度向右射向放在光滑地面上静止的质量为2kg的物块．
如图所示，质量为m1=2.0kg、长为L=10.0m的平板小车，静止在光滑水平地面上，一质量为m2=0.5kg的小物块以v0=10.0m/s速度从左端冲上平板车，已知小物块与平板车之间的动摩擦因数μ=0.30．有关平板车和小物块最后的速度v'1和v'2的大小，以及整个过程中系统内能的增加量Q的计算试，正确的是（g=10m/s2）（ ）A、v′1=v′2=
| ||||||
B、v′1=v′2=
| ||||||
C、v′1＜
| ||||||
D、v′1＜
|
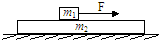（2011?河南模拟）如图所示，质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行，长木板保持静止状态．已知木块与长木板间的动摩擦因数为μ1，长木板与水平地面间的动摩擦因数为μ2，则（ ）
（2009?崇文区一模）如图所示，质量为m1=1kg的小物块P置于桌面上的A点并与弹簧的右端接触（不拴接），轻弹簧左端固定，且处于原长状态．质量M=3.5kg、长L=1.2m的小车静置于光滑水平面上，其上表面与水平桌面相平，且紧靠桌子右端．小车左端放有一质量m2=0.5kg的小滑块Q．现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内）时，撤去推力，此后P沿桌面滑到桌子边缘C时速度为2m/s，并与小车左端的滑块Q相碰，最后Q停在小车的右端，物块P停在小车上距左端0.5m处．已知AB间距离L1=5cm，AC间距离L2=90cm，P与桌面间动摩擦因数μ1=0.4，P、Q与小车表面间的动摩擦因数μ2=0.1，（g取10m/s2），求：