题目内容

【题目】如图所示，在内壁光滑的平底试管内放一个质量为1 g的小球，试管的开口端与水平轴O连接．试管底与O相距5 cm，试管在转轴带动下在竖直平面内做匀速圆周运动．求：

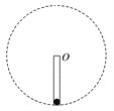
(1)转轴的角速度达到多大时，试管底所受压力的最大值等于最小值的3倍？

(2)转轴的角速度满足什么条件时，会出现小球与试管底脱离接触的情况？(g取10 m/s2)

【答案】(1)20 rad/s　(2)

【解析】试题分析:（1）在最高点时对试管的压力最小，根据向心力公式有：mg+Nmin=mω2r

在最低点时对试管的压力最大，根据向心力公式有：Nmax-mg=mω2r

因为Nmax=3Nmin

所以解得：ω=20rad/s；

（2）当小球对试管的压力正好等于0时，小球刚好与试管分离，根据向心力公式得：mg=mω02r

解得：ω0＝10rad/s

所以当ω＜10rad/s时会脱离接触

练习册系列答案
相关题目

【题目】图示是磁带录音机的磁带盒示意图，A、B为缠绕磁带的两个轮子，半径均为r.在放音结束时，磁带全部绕到了B轮上，磁带的外缘半径为R，且R＝3r. 现在进行倒带，使磁带绕到A轮上；倒带时A轮是主动轮，其角速度是恒定的，B轮是从动轮，经测定磁带全部绕到A轮上需要的时间为t，则从开始倒带到A、B两轮的角速度相等所需要的时间应是(　　)

A. 等于 B. 大于

C. 小于 D. 无法确定

【题目】在某次实验中，物体拖动纸带做匀加速直线运动，打点计时器所用的电源频率为50Hz，实验得到的一条纸带如下图所示，纸带上每相邻的两个计数点之间都有4个点未画出。按时间顺序取0、1、2、3、4、5六个计数点，实验中用直尺量出各计数点到0点的距离如下图所示（单位：cm）

（1）在计数点1所代表的时刻，纸带运动的瞬时速度为v1= _______m/s（保留两位有效数字），物体的加速度a= _______m/s2（保留两位有效数字）

（2）该同学在测量的时候没有将计数点5的数值记录下来，根据前面的数值可以推算出计数点5到0点的距离为_______cm。（保留四位有效数字）

【题目】如图所示，一辆车做匀加速直线运动，车厢中放置一固定斜面，分别在斜面和水平面上固定内壁光滑的细管，将两个劲度系数相同的轻质弹簧一端分别固定在两细管右端，另一端连接质量相同的小球，小球的直径略小于细管的内径。两弹簧的劲度系数均为k。某时刻侧得水平细管中弹簧的伸长量为x1，倾斜细管中弹簧的伸长量x2，当地重力加速度为g。已知mg，=mg，则下列选项正确的是

A. 车的加速度a=g

B. 车的加速度

C. 斜面倾角θ=60°

D. 料面倾角θ=30°

【题目】圆形导体环用一根轻质细杆悬挂在O点，导体环可以在竖直平面里来回摆动，空气阻力和摩擦力均可不计．在图所示的正方形区域里，有匀强磁场垂直于圆环的振动面指向纸内．下列说法中正确的有(　 　)

A. 此摆振动的开始阶段机械能不守恒

B. 导体环进入磁场和离开磁场时，环中电流的方向肯定相反

C. 导体环通过最低点时，环中感应电流最大

D. 最后此摆在匀强磁场中振动时，机械能守恒

【题目】用如图甲所示装置做“验证机械能守恒定律”实验。

（1）必须用到的测量仪器是__________

A.秒表 B.刻度尺 C.弹簧测力计 D.天平

（2）如图乙所示，为实验中的一条纸带，根据纸带上已测出的数据，可得打“5”点时重物的速度为

v5=________m/s；取刚下落时重物所在位置为零势能面，可得出打“5”点时重物的重力势能为EP=_______J，此时重物的机械能E5=________J（电源频率为50Hz，重物质量为mkg）

（3）同样的办法计算得到打6点时重物的机械能E6，发现E6<E5，造成该误差的主要因素是______________________________________________

【题目】如图所示，倾角，长l=2.7m的光滑斜面固定在水平地面上，质量为3m的小物体A和质量为m的物体B分别系在轻绳两端，绳子跨过固定在斜面顶端的轻质滑轮，开始时把物体B拉到斜面底端并固定，这时物体A离地面的高度h=1.6m，重力加速度为g，sin37°=0.6。求：

(1)使B静止所需的最小力；

(2)由静止释放B，求A落地前B运动的加速度大小；

(3)若斜面不光滑，自斜面底端由静止释放B，B撞不到定滑轮，求B与斜面间动摩擦因数的最小值。

【题目】如图所示的装置叫做阿特伍德机，是阿特伍德创制的一种著名力学实验装置，用来研究匀变速直线运动的规律。绳子两端的物体下落（或上升）的加速度总是小于自由落体的加速度g。已知物体A、B的质量相等均为4m，物体C的质量为m，一切摩擦不计，轻绳不可伸长且足够长， 现将装置从静止释放。下列说法正确的是

A. 物体C的加速度为 B. 物体C的加速度为

C. 物体C对B的拉力为 D. 物体C对B的拉力为

【题目】某实验小组利用如图（1)所示的装置探究加速度与力质量的关系。

(1) 下列做法正确的是_______(填字母代号)。

A.调节滑轮的高度，使牵引小车的细绳与长术板保持平行

B.在平衡小车受到的摩擦力时，将装有砝码的砝码柏通过定滑轮拴在小车上

C.实验时，先放开小车再接通打点计时器的电源

D.通过增减小车上的砝码改变质量时，不需要重新调节木板的倾斜度

(2)若保持砝码和砝码桶质量m不变，改变小车质量M，分别得到小车加速度a与质量M及对应的数据如表所示请在图(2)所示的方格坐标纸中并作出a-图线。从图线中得到F不变时，小车加速度a与质量M之间存在的关系式子是________。

(3)某同学在探究a 与F的关系时，把砝码和砝码桶的总重力当作小车的合外力F，作出a-F图线如图（3）所示，试分析图线不过原点的原因是______________。

(4)在这个实验中，为了探究两个物理量之间的关系，要保持第三个物理量不变，这种探究方法叫做_____________。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网