题目内容
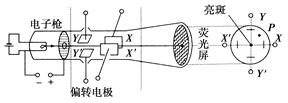
如图所示的装置放置在真空中,炽热的金属丝可以发射电子,金属丝和竖直金属板之间加以电压U1=2500V,发射出的电子被加速后,从金属板上的小孔S射出.装置右侧有两个相同的平行金属极板水平正对放置,板长l=6.0cm,相距d=2cm,两极板间加以电压U2=200V的偏转电场.从小孔S射出的电子恰能沿平行于板面的方向由极板左端中间位置射入偏转电场.已知电子的电荷量e=1.6×10-19C,电子的质量m=0.9×10-30kg,设电子刚离开金属丝时的速度为0,忽略金属极板边缘对电场的影响,不计电子受到的重力.求:
(1)电子射入偏转电场时的动能Ek;
(2)电子射出偏转电场时在竖直方向上的侧移量y;
(3)电子在偏转电场运动的过程中电场力对它所做的功W.

(1)电子射入偏转电场时的动能Ek;
(2)电子射出偏转电场时在竖直方向上的侧移量y;
(3)电子在偏转电场运动的过程中电场力对它所做的功W.

(1)电荷量为e的电子从金属丝移动到金属板,两处的电势差为U1,电势能的减少量是eU1,减少的电势能全部转化为电子的动能,所以:
eU1=Ek
解得:
Ek=eU1=1.6×10-19×2500=4×10-16V
(2)电子在垂直于板面的方向受到静电力,由于电场不随时间改变,而且是匀强电场,所以整个运动过程中在垂直于板面的方向上加速度是不变的,做匀加速直线运动,加速度是:
a=
=
电子射出电场时,在垂直于板面方向偏移的距离为:
y=
at2
其中t为飞行时间,由于电子在平行于板面的方向不受力,所以这个方向上做匀速运动,由 l=v0t可求得:
t=
将a和t代入y的表达式中,得到:
y=
?
?(
)2
将Ek=
m
代入得:
y=
代入数值后,得:
y=
=0.0036m=0.36cm
即电子射出电场时沿垂直于板面方向偏移的距离0.36cm;
(3)电子在偏转电场运动的过程中电场力对它所做的功为:
W=qEy=
=
=5.76×10-18J
答:(1)电子射入偏转电场时的动能为4×10-16J;
(2)电子射出偏转电场时在竖直方向上的侧移量y为0.36cm;
(3)电子在偏转电场运动的过程中电场力对它所做的功W为4×10-16J.
eU1=Ek
解得:
Ek=eU1=1.6×10-19×2500=4×10-16V
(2)电子在垂直于板面的方向受到静电力,由于电场不随时间改变,而且是匀强电场,所以整个运动过程中在垂直于板面的方向上加速度是不变的,做匀加速直线运动,加速度是:
a=
| F |
| m |
| eU2 |
| md |
电子射出电场时,在垂直于板面方向偏移的距离为:
y=
| 1 |
| 2 |
其中t为飞行时间,由于电子在平行于板面的方向不受力,所以这个方向上做匀速运动,由 l=v0t可求得:
t=
| l |
| v0 |
将a和t代入y的表达式中,得到:
y=
| 1 |
| 2 |
| eU2 |
| md |
| l |
| v0 |
将Ek=
| 1 |
| 2 |
| v | 20 |
y=
| U2l2 |
| 4dU1 |
代入数值后,得:
y=
| 200×0.062 |
| 4×0.02×2500 |
即电子射出电场时沿垂直于板面方向偏移的距离0.36cm;
(3)电子在偏转电场运动的过程中电场力对它所做的功为:
W=qEy=
| qU2y |
| d |
| 1.6×10-19×200×0.0036 |
| 0.02 |
答:(1)电子射入偏转电场时的动能为4×10-16J;
(2)电子射出偏转电场时在竖直方向上的侧移量y为0.36cm;
(3)电子在偏转电场运动的过程中电场力对它所做的功W为4×10-16J.

练习册系列答案
相关题目