题目内容
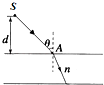
【题目】在匀强磁场中有一个静止的氡原子核( ![]() Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个互相外切的圆,大圆与小圆的直径之比为42:1,如图所示,那么氡核的衰变方程应是下列方程中的哪一个( )
Rn),由于衰变它放出一个粒子,此粒子的径迹与反冲核的径迹是两个互相外切的圆,大圆与小圆的直径之比为42:1,如图所示,那么氡核的衰变方程应是下列方程中的哪一个( )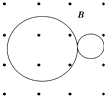
A.![]() Rn→
Rn→ ![]() Fr+
Fr+ ![]() e
e
B.![]() Rn→
Rn→ ![]() Po+
Po+ ![]() He
He
C.![]() Rn→
Rn→ ![]() At+
At+ ![]() e
e
D.![]() Rn→
Rn→ ![]() At+
At+ ![]() e
e
【答案】B
【解析】解:粒子在磁场中做匀速圆周运动,根据牛顿第二定律,有:
qvB=m ![]()
故r= ![]()
粒子衰变过程中不受外力,系统动量守恒,故生成的两个粒子的动量mv等大、反向,故:
r= ![]() ∝
∝ ![]()
大圆与小圆的直径之比为42:1,故生成的两个粒子的电荷量之比为1:42;
根据电荷数守恒守恒,生成物是α粒子,故ACD不符合题意,B符合题意;
所以答案是:B
【考点精析】根据题目的已知条件,利用动量守恒定律的相关知识可以得到问题的答案,需要掌握动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

练习册系列答案
相关题目