题目内容
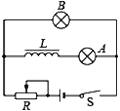
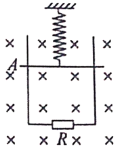
【题目】在水平向里,磁感应强度为B的匀强磁场中竖直放置两根间距为L的光滑金属导轨,底端接电阻R,轻弹簧上端固定,下端悬挂质量为m,电阻为r的金属棒,金属棒和导轨接触良好,导轨电阻不计。金属棒静止时位于A处。现将金属棒从弹簧原长位置由静止释放,金属棒在运动过程中始终保持水平,弹簧的劲度系数为k,重力加速度为g。则下列说法正确的是
A. 金属棒向下运动时通过R的电流方向是从右向左
B. 金属棒第一次到达A处时速度最大
C. 金属棒能到达的最低点在A位置下方![]() 处
处
D. 金属棒从释放到第一次下降到A位置的过程中,通过电阻R的电荷量为![]()
【答案】AD
【解析】
根据楞次定律右手定则可判断感应电流的方向;金属棒运动过程中,经过平衡位置时,即加速度为零时速度最大;金属棒运动过程中,存在电磁阻尼,做阻尼振动,振幅越来越小;利用平均电流来计算电荷量,即![]() 。
。
A、根据楞次定律右手定则,流过回路的电流为顺时针方向,即流过电阻R的电流方向从右向左,A正确;
B、金属棒经过平衡位置时速度最大,在平衡位置,金属棒受到的弹簧弹力和同方向安培力的合力与重力等大反向,三力平衡,故速度最大的位置高于A点,B错误;
C、金属棒静止在A位置时,![]() ,弹簧形变量为
,弹簧形变量为![]() ,现将金属棒从原长位置释放,由于存在电磁阻尼,金属棒振幅越来越小,故金属棒不可能到达关于A点对称的在A点下方
,现将金属棒从原长位置释放,由于存在电磁阻尼,金属棒振幅越来越小,故金属棒不可能到达关于A点对称的在A点下方![]() 处,故C错误;
处,故C错误;
D、金属棒从原长位置运动到A点的过程中,磁通量的变化量为![]() ,则该过程中通过电阻R的电荷量
,则该过程中通过电阻R的电荷量![]() ,得
,得![]() ,故D正确。
,故D正确。
故本题选AD。

练习册系列答案
相关题目