题目内容
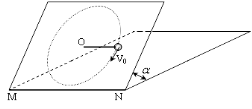
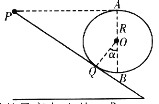
【题目】如图是过山车的部分模型图。模型图中光滑圆形轨道的半径R=8.1m，该光滑圆形轨道固定在倾角为
斜轨道面上的Q点，圆形轨道的最高点A与P点平齐，圆形轨道与斜轨道之间圆滑连接。现使小车(视作质点)从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为
，不计空气阻力，过山车质量为20kg，取g=10m／s2，
。若小车恰好能通过圆形轨道的最高点A处，求：
(1)小车在A点的速度为多大；
(2)小车在圆形轨道的最低点B时对轨道的压力为重力的多少倍；
(3)小车在P点的动能．
【答案】（1）9m/s；（2）6；（3）1290J
【解析】
试题分析：（1）小车恰好能通过最高点A，说明在A点小车只受重力作用，根据合力提供向心力有：
得小球在A点的速度为：
（2）小车从B至A的过程中只有重力对小车做功，根据动能定理有：
得小车在B点时的速度为：
小车在B点所受轨道支持力和重力的合力提供圆周运动向心力，令小车质量为mkg有：
解得：N＝60mN
小车的受到轨道支持力为其重力的6倍．根据牛顿第三定律知，小车对轨道的压力为其重力的6倍；
（3）设Q点与P点的高度差为h，PQ间的距离为L，则由几何关系有：
小车从P到A，由动能定理有：
得：v0＝
m/s
则小车在P点的动能
【题目】小明同学在学完力的合成与分解后，想在家里做实验验证力的平行四边形定则．他从学校的实验室里借来两只弹簧测力计，按如下步骤进行实验．
A．在墙上贴一张白纸用来记录弹簧弹力的大小和方向 |
B．在一只弹簧测力计的下端悬挂一装满水的水杯，记下静止时弹簧测力计的读数F． |
C．将一根大约30cm长的细线从杯带中穿过，再将细线两端拴在两只弹簧测力计的挂钩上．在靠近白纸处用手对称地拉开细线，使两只弹簧测力计的读数相等，在白纸上记下细线的方向和弹簧测力计的读数．如图甲所示． |
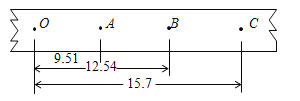
D．在白纸上按一定标度作出两个弹簧测力计的弹力的图示（两弹力夹角为60度），如图乙所示，根据力的平行四边形定则可求出这两个力的合力F′． |
（1）在步骤C中，弹簧测力计的读数为 N．
（2）在步骤D中，合力F′= N．（保留2位有效数字）
（3）若 ，就可以验证力的平行四边形定则．
