题目内容
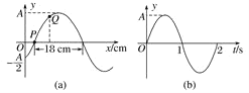
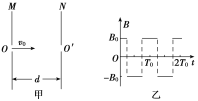
【题目】如图甲所示,M、N为竖直放置彼此平行的两块平板,板间距离为d,两板中央各有一个小孔O、O′正对,在两板间有垂直于纸面方向的磁场,磁感应强度随时间的变化如图乙所示,设垂直纸面向里的磁场方向为正方向。有一群正离子在t=0时垂直于M板从小孔O射入磁场。已知正离子质量为m、带电荷量为q,正离子在磁场中做匀速圆周运动的周期与磁感应强度变化的周期都为T0,不考虑由于磁场变化而产生的电场的影响。求:
(1)磁感应强度B0的大小;
(2)要使正离子从O′孔垂直于N板射出磁场,正离子射入磁场时的速度v0的可能值。
【答案】(1)![]() ,(2)
,(2)![]() (n=1,2,3…)。
(n=1,2,3…)。
【解析】
(1)正离子射入磁场,由洛伦兹力提供向心力,即:
qv0B0=![]()
做匀速圆周运动的周期:
T0=![]()
联立两式得磁感应强度:B0=![]() ;
;
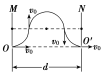
(2)要使正离子从O′孔垂直于N板射出磁场,两板之间正离子只运动一个周期即T0时,v0的方向应如图所示,有:
r=![]()
当在两板之间正离子共运动n个周期,即nT0时,有
r=![]() (n=1,2,3…)
(n=1,2,3…)
联立方程求解,得正离子的速度的可能值为:
v0=![]() =
=![]() (n=1,2,3…)
(n=1,2,3…)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目