Question

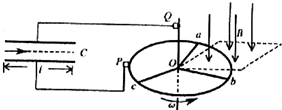如图所示，半径为r的金属圆环置于水平面内，三条电阻均为R的导体杆Oa、Ob和Oc互成120°连接在圆心O和圆环上，圆环绕经过圆心O的竖直金属转轴以大小为ω的角速度按图中箭头方向匀速转动．一方向竖直向下的匀强磁场区与圆环所在平面相交，相交区域为一如图虚线所示的正方形（其一个顶点位于O处）．C为平行板电容器，通过固定的电刷P和Q接在圆环和金属转轴上，电容器极板长为l，两极板的间距为d．有一细电子束沿两极板间的中线以大小为v₀（v0＞

2ωl

π

）的初速度连续不断地射入C．
（1）射入的电子发生偏转时是向上偏转还是向下偏转？
（2）已知电子电量为e，质量为m．忽略圆环的电阻、电容器的充电放电时间及电子所受的重力和阻力．欲使射入的电子全部都能通过C所在区域，匀强磁场的磁感应强度B应满足什么条件？

Answer 1

分析：（1）题中三个导体杆做切割磁感线，产生感应电动势，根据右手定则判断感应电动势的方向，确定出两金属板电势的高低，即可判断电子的偏转方向．
（2）电子进入电容器C后，某一导体棒也开始进入磁场，电子电子做类平抛运动，在水平方向不受电场力而做匀速直线运动，在竖直方向受到电场力而做匀加速运动；在没有电场的时间内竖直方向做匀速直线运动，根据牛顿第二定律和运动学公式结合求出电子在竖直方向的最大位移y，要使射入的电子全部都能通过电容器C，必须满足的条件是y≤

d

2

，联立可求出磁感应强度B的范围．

解答：解：（1）根据右手定则判断可知，三个导体杆产生的感应电动势都指向O点，O点相当于电源的正极，则电容器上板电势高于下板电势，电场方向向下，故射入的电子发生偏转时是向上偏转．                         ①
（2）当导体杆处于磁场中时，感应电动势 E=Br

.

v

②
导体杆转动的平均速度

.

v

=

1

2

r?ω
所以，E=

1

2

Br2ω ③
此时，磁场中导体杆的电阻为内电阻，其余的电阻为外电阻，电容器的电压 U=

R/2

R+R/2

E=

1

3

E④
射入的电子在两极板间运动　l=v₀t⑤
因为v0＞

2ωl

π

，所以t＜

π

2ω

⑥
而

π

2ω

就是每条导体杆在磁场中运动的时间，因此有部分电子在两极板间运动的时间内，极板间的电场始终存在，这部分电子在极板间的偏转量最大．
设电子恰好能离开通过C，有

d

2

=

1

2

at2⑦
而　　　a=

eU

md

⑧
由以上各式得　B=

6m v 2 0 d2

eωr2l2

⑨
磁感强度B应满足的条件是　B＜

6m v 2 0 d2

eωr2l2

⑩
答：
（1）射入的电子发生偏转时向上偏转．
（2）欲使射入的电子全部都能通过C所在区域，匀强磁场的磁感应强度B应满足的条件是：B＜

6m v 2 0 d2

eωr2l2

．

点评：本题是电磁感应与电路、电场知识的综合，关键是根据牛顿第二定律和运动学公式求出电子在竖直方向的最大位移y，可以运用v_y-t图象分析电子在竖直方向的运动情况，便于理解．