题目内容
4.质量为m的卫星发射前静止在地球赤道表面.假设地球可视为质量均匀分布的球体,半径为R.(1)已知地球质量为M,自转周期为T,引力常量为G.求此时卫星对地表的压力N的大小;
(2)卫星发射后先在近地轨道上运行(轨道离地面的高度可以忽略不计),运行的速度大小为v1,之后经过变轨成为地球的同步卫星,此时离地面高度为H,运行的速度大小为v2.
a.求比值$\frac{{V}_{1}}{{V}_{2}}$;
b.若卫星发射前随地球一起自转的速度大小为v0,通过分析比较v0、v1、v2三者的大小关系.
分析 (1)卫星静止在地球上,随地球一起做匀速圆周运动,根据牛顿第二定律求解卫星对地表的压力N的大小;
(2)a、卫星围绕地球做匀速圆周运动,根据万有引力提供向心力求出线速度之比;
b、同步卫星与地球自转的角速度相等,而半径大于地球半径,据此分析v0和v2的关系,结合a的结论分析三者之间的关系.
解答 解:(1)卫星静止在地球上,随地球一起做匀速圆周运动,根据牛顿第二定律得:
$G\frac{Mm}{{R}^{2}}-N′=m\frac{4{π}^{2}R}{{T}^{2}}$
解得:N′=$G\frac{Mm}{{R}^{2}}-m\frac{4{π}^{2}R}{{T}^{2}}$
根据牛顿第三定律可知卫星对地表的压力N的大小为:
N=N′=$G\frac{Mm}{{R}^{2}}-m\frac{4{π}^{2}R}{{T}^{2}}$
(2)a、卫星围绕地球做匀速圆周运动,万有引力提供向心力,则有:
$G\frac{Mm}{{R}^{2}}=m\frac{{{v}_{1}}^{2}}{R}$,
$G\frac{Mm}{{(R+H)}^{2}}=m\frac{{{v}_{2}}^{2}}{(R+h)}$,
解得:$\frac{{v}_{1}}{{v}_{2}}=\sqrt{\frac{R+H}{R}}$
b、同步卫星与地球自转的角速度相等,而半径大于地球半径,根据v=ωr可知,v2>v0,而v1>v2,所以v1>v2>v0.\
答:(1)此时卫星对地表的压力N的大小为$G\frac{Mm}{{R}^{2}}-m\frac{4{π}^{2}R}{{T}^{2}}$;
(2)a.$\frac{{v}_{1}}{{v}_{2}}$的值为$\sqrt{\frac{R+H}{R}}$;
b.v0、v1、v2三者的大小关系为v1>v2>v0.
点评 本题考查万有引力在天体运动中的应用,要注意分清是卫星是绕地球运动,还是静止在地面上,明确在地球上与卫星运动向心力是不同的.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案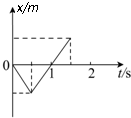
| A. | 在0到1 s时间内该质点的平均速率为零 | |
| B. | 在0到1 s时间内t=1 s时该质点回到出发点 | |
| C. | 在0到1 s时间内t=1 s时该质点瞬时速度为零 | |
| D. | 在0到1 s时间内t=0.5 s时该质点离出发点最远 |
| A. | β射线的电离作用最强 | B. | γ射线的电离作用最强 | ||
| C. | α射线的穿透能力最强 | D. | γ射线的穿透能力最强 |
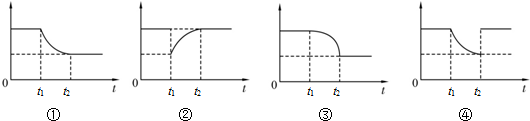
| A. | ①图描述了汽车的速度在这个过程中随时间的变化情况 | |
| B. | ②图描述了汽车的速度在这个过程中随时间的变化情况 | |
| C. | ③图描述了汽车的牵引力在这个过程中随时间的变化情况 | |
| D. | ④图描述了汽车的牵引力在这个过程中随时间的变化情况 |
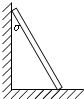 如图所示,一架梯子斜靠在光滑竖直墙和粗糙水平面间静止,梯子和竖直墙的夹角为α.当α再增大一些后,梯子仍然能保持静止.那么α增大后和增大前比较,下列说法中正确的是( )
如图所示,一架梯子斜靠在光滑竖直墙和粗糙水平面间静止,梯子和竖直墙的夹角为α.当α再增大一些后,梯子仍然能保持静止.那么α增大后和增大前比较,下列说法中正确的是( )| A. | 地面对梯子的支持力增大 | B. | 墙对梯子的支持力减小 | ||
| C. | 水平面对梯子的摩擦力增大 | D. | 梯子受到的合外力增大 |
| A. | 末速度比初速度小3m/s | B. | 末速度比初速度大3m/s | ||
| C. | 加速度方向与初速度方向相同 | D. | 末速度方向与初速度方向相反 |
 如图一个质量为M、倾角为θ的楔状斜面体A,放在粗糙的水平面,斜面上有一个质量为m的物体B沿斜面匀速下滑.求地面对A的摩擦力和支持力分别多大?
如图一个质量为M、倾角为θ的楔状斜面体A,放在粗糙的水平面,斜面上有一个质量为m的物体B沿斜面匀速下滑.求地面对A的摩擦力和支持力分别多大?