题目内容
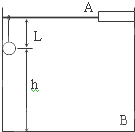
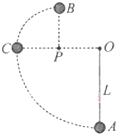
如图所示,质量为m的小球用长为L的轻质细绳悬于O点,与O点处于同一水平线上的P点处有一个光滑的细钉,已知OP=
L.在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B(重力加速度为g).则以下说法正确的是( )
| 1 |
| 2 |
| A.小球到达B点时的速度为零 | ||||
B.若不计空气阻力,则初速度v0=
| ||||
| C.若不计空气阻力,小球在最低点A时,绳子的拉力为4.5mg | ||||
D.若初速度v0=3
|

A、据题小球恰能最高点B,由重力提供小球圆周运动所需的向心力,根据牛顿第二定律得:mg=m
| ||
|
|
B、若不计空气阻力,从A到B,由动能定理得:-mg?
| 3 |
| 2 |
| 1 |
| 2 |
| v | 2B |
| 1 |
| 2 |
| v | 20 |
|
C、若不计空气阻力,小球在最低点A时,根据牛顿第二定律得:T-mg=m
| ||
| L |
D、若初速度v0=3
| 3gL |
| 3 |
| 2 |
| 1 |
| 2 |
| v | 2B |
| 1 |
| 2 |
| v | 20 |
| 11 |
| 4 |
故选:CD

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目