题目内容
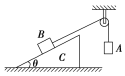
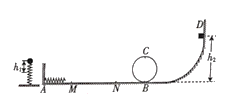
【题目】将一轻质弹簧竖直固定在水平地面上处于原长状态,让一质量m=20g的小球从弹簧上端由静止释放,小球最大下落高度h1=5cm,将该弹簧固定在如图所示的轨道左侧竖直墙壁上,轨道中部有一半径R=0.1m的竖直圆轨道,不同轨道的连接处均为平滑连接,小滑块可以从圆轨道最低点的一侧进入圆轨道,绕圆轨道一周后从最低点向另一侧运动。轨道上弹簧右侧的M点到圆轨道左侧N点的距离xMN=0.6m的范国内有摩擦,而其他部分均光滑。让另一质量m=10g的小滑块从轨道右侧高h2(未知)处由静止释放,小滑块恰好能通过圆轨道最高点C,且第一次恰好能把弹簧压缩5cm,现让该小滑块从轨道右侧高h3=0.4m处由静止释放,已知重力加速度g=10m/s2,求
(1)小滑块下落的高度h2;
(2)小滑块停止时的位置到N点的距离
【答案】(1)0.25m(2)0.4m
【解析】
小滑块恰好能过C点,根据牛顿第二定律和机械能守恒定律可得小滑块下落的高度h2;弹簧竖直放置,求出被压缩h1=5cm时的弹性势能,在根据动能定理即可求出小滑块停止时的位置到N点的距离。
(1)小滑块恰好能过C点,根据牛顿第二定律可得:![]()
由机械能守恒定律可得:![]()
解得:![]()
(2)弹簧竖直放置,被压缩h1=5cm时的弹性势能![]() .
.
由动能定理可知,从小滑块第一次滑至第一次把弹簧压缩到最短时有:![]() ,其中
,其中![]()
解得:![]()
当小滑块从h3=0.4m处下滑后,第二次通过N点时的动能为:
![]()
此时小滑块动能小于0.015J,故小滑块不在与弹簧相碰
由动能定理可得:![]()
解得:![]()
小滑块最终停在N点左侧0.4m处。

练习册系列答案
相关题目