Question

如图所示，长l的轻直杆两端分别固定小球A和B，A、B都可以看作质点，它们的质量分别为2m和m．A球靠在光滑的竖直墙面上，B球放置在光滑水平地面上，杆与竖直墙面的夹角为37°．现将AB球由静止释放，A、B滑至杆与竖直墙面的夹角为53°时，V_A：V_B=______，A球运动的速度大小为______．（已知sin37°=0.6，cos37°=0.8）

Answer 1

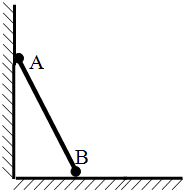
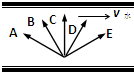
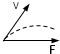
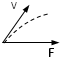
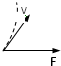
根据题意，将A球速度分解成沿着杆与垂直于杆方向，同时B球速度也是分解成沿着杆与垂直于杆两方向．
则有，A球：v_⊥=v_Asinα v_∥=v_Acosα
而B球，

v

′⊥

=vBsinβ

v

′∥

=vBcosβ
由于同一杆，则有v_Acosα=v_Bcosβ
又因α=53°，β=37° 所以v_A：v_B=4：3；
将AB球由静止释放，A、B滑至杆与竖直墙面的夹角为53°时，
根据动能定理可知，2mg（lcos37°-lcos53°）=

1

2

2m

v

2A

+

1

2

m

v

2B

解得：vA=8

gl 205

故答案为：4：3，8

gl 205