题目内容
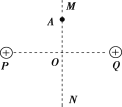
【题目】天文学家哈雷曾经在1682年跟踪过一颗彗星，它算出这颗彗星轨道的半长轴约等于地球公转半径的18倍，并预言这颗彗星将每隔一定时间就会出现，后来哈雷的预言得到证实，该彗星被命名为哈雷彗星。如图所示为哈雷彗星绕太阳运行的椭圆轨道，P为近日点，Q为远日点，M、N为轨道短轴的两个端点。若只考虑哈雷彗星和太阳之间的相互作用，则
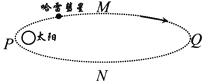
A. 哈雷彗星的运行周期约为76年
B. 哈雷彗星从P点运动到M点需要19年
C. 哈雷彗星从P经M到Q阶段，速率逐渐减小
D. 哈雷彗星从P经M到Q阶段，机械能逐渐减小
【答案】AC
【解析】
设彗星的周期为T1，地球的公转周期为T2，这颗彗星轨道的半长轴约等于地球公转半径的18倍，由开普勒第三定律
得：
，即
年，A正确；从P到Q过程中，需要克服引力做功，动能减小，即速度越来越小，所以从P到M过程中小于周期的四分之一，即小于19年，B错误C正确；过程中只有引力做功，机械能不变，D错误．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
