题目内容
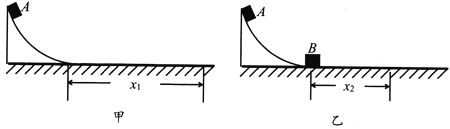
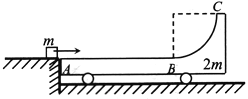
【题目】如图所示，质量为2m的小车紧靠平台的边缘静止在光滑的水平面上，小车AB段是长为L的水平粗糙轨道，BC段是四分之一圆弧光滑轨道，两段轨道相切于B点。小车AB段轨道与平台在同一水平面上。质量为m的滑块(可视为质点)沿着光滑的平台以某一速度向右运动并滑上小车，若滑块与AB段轨道间的动摩擦因数为μ，重力加速度为g。
(1)使滑块不滑过B点，则滑块在平台上运动的速度v不超过多大?
(2)当滑块在平台上运动的速度为
时，恰好能到达C点，则BC段圆弧轨道的半径R是多大?
【答案】(1) 
(2) 2μL
【解析】
（1）若滑块在平台上运动的速度为v时，恰好滑到小车的B点，此时滑块和小车的共同速度为
，
地面光滑，满足动量守恒的条件，有
，解得
，
由功能关系，该过程中产生的内能
，
减少的动能
，
已知减少的动能全部转化为内能，联立可得
即滑块在平台上运动的速度v不超过
（2）当滑块在平台上运动的速度
时，恰好能到达C点，即滑块和小车恰好达到共同速度，设此时速度为
，根据动量守恒定律
，解得
；
该过程减少的动能
，
增加的内能和重力势能
，
系统减少的动能全部转化为内能和重力势能，联立可得
．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
