Question

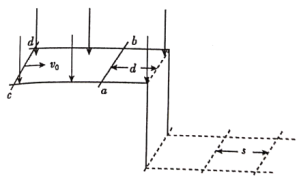
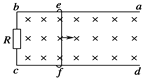
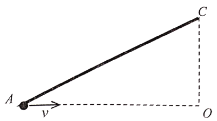
【题目】如图在光滑绝缘平面上有一直角三角形区域AOC，AC上放置一个绝缘材料制成的固定挡板，其长度AC＝L，∠A＝30°，现有一个质量为m，带电量为+q可视为质点的小球从A点，以初速度v沿AO方向运动。小球与挡板的碰撞均为弹性碰撞（打到C点时也记一次碰撞），且不计一切摩擦和碰撞时间。若在AOC区域施加一个垂直水平面向里的匀强磁场，则:

（1）要使小球能到达C点，求磁感应强度的最小值Bmin

（2）要使小球能到达C点，求小球与AC边碰撞次数n和磁感应强度大小B应满足的条件若在AOC区域施加一个沿O到C方向的匀强电场，则:

（3）要使小球能到达C点，求电场强度的最小值Emin

（4）要使小球能到达C点，求小球与AC边碰撞次数和电场强度大小E应满足的条件

Answer 1

【答案】（1）（2），其中nN※（3）（4）

【解析】

（1）根据几何关系可知粒子能够运动到C点的最大半径为r=L

根据

解得：

Bmin=

（2）粒子与板发生n次碰撞所对应的轨道半径为：

根据

解得：

Bmin=其中nN※

（3）在区间加竖直向上的电场时，且带电粒子做一次类平抛运动到C点时电场强度最小，水平方向上：

竖直方向上：

LOC=

解得：：

’Emin=

（4）将电场力沿平行AC和垂直AC分解

a平行=

a垂直=

沿AC方向的运动是初速度为v平行=，加速度为a平行=的匀加速直线运动

得到L=v平行t+a平行t2=t+

所以

t=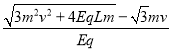

得

n=

即

n=