Question

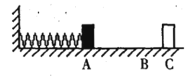
【题目】静止在光滑水平面上的平板车B的质量为m=0.5kg、长L=1m．某时刻A以v0=4m/s向右的初速度滑上木板B的上表面，物体A的质量M=1kg，在A滑上B的同时，给B施加一个水平向右的拉力．忽略物体A的大小，已知A与B之间的动摩擦因数=0.2，取重力加速度g=10m/s2．试求

（1）若F=5N，物体A在小车上运动时相对小车滑行的最大距离；

（2）如果要使A不至于从B上滑落，拉力F大小应满足的条件．

Answer 1

【答案】（1）物体A在小车上运动时相对小车滑行的最大距离为0.5m．

（2）拉力F大小应满足的条件为1N≤F≤3N

【解析】试题分析：（1）物块滑上平板车，物块做匀减速运动，小车做匀加速直线运动，当两者速度相同时，物块在小车上相对运动的距离最大，结合牛顿第二定律和运动学公式求出物体A在小车上运动时相对小车滑行的最大距离．

（2）物体A不滑落的临界条件是A到达B的右端时，A、B具有共同的速度，结合牛顿第二定律和运动学公式求出拉力的最小值．另一种临界情况是A、B速度相同后，一起做匀加速直线运动，根据牛顿第二定律求出拉力的最大值，从而得出拉力F的大小范围．

解：（1）物体A滑上木板B以后，作匀减速运动，

有Mg=MaA得

aA=g="0.2×10=2" m/s2

平板车B作加速运动，有F+Mg=maB，

代入数据解得：aB="14" m/s2

两者速度相同时，有V0﹣aAt=aBt，

代入数据解得：t=0.25s

A滑行距离：SA=V0t﹣aAt2=4×0.25﹣×=m

B滑行距离：SB=aBt2=×=m

最大距离：△s=SA﹣SB=m﹣m=0.5m．

由于△xm＜1m，以上分析和结论成立

（2）物体A不滑落的临界条件是A到达B的右端时，A、B具有共同的速度v1，则：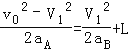

又：，

可得：aB=6m/s2

再代入F+Mg=maB得：

F=maB﹣Mg=0.5×6﹣0.2×1×10=1N

若F＜1N，则A滑到B的右端时，速度仍大于B的速度，于是将从B上滑落，所以F必须大于等于1N．

当F较大时，在A到达B的右端之前，就与B具有相同的速度，之后，A必须相对B静止，才不会从B的左端滑落．即有：F=（m+M）a，

m1g=m1a

所以：F=3N

若F大于3N，A就会相对B向左滑下．

综上所述，力F应满足的条件是：1N≤F≤3N

答：（1）物体A在小车上运动时相对小车滑行的最大距离为0.5m．

（2）拉力F大小应满足的条件为1N≤F≤3N