题目内容
14.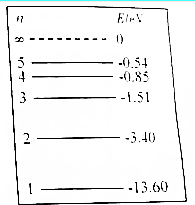 已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)
已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)A:一个具有Eko=13.60eV动能、处于基态的氢原子与一个静止的同样出于基态的氢原子发生对心碰撞,可能跃迁到n=2能级的第一个激发态
B:一个具有Eko=13.60eV动能、处于基态的氢原子与一个静止的同样出于基态的氢原子发生对心碰撞,原子不可能跃迁到其他激发态
C:用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子能跃迁到n=2能级的轨道上去
D:用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子不能跃迁到其他轨道上去
E:用动能为12.3eV的电子去照射一群处于基态的氢原子,氢原子受电子照射后,原子能跃迁到n=2能级的轨道上去.
分析 根据碰撞过程中的动量守恒与能量守恒求解碰撞前运动氢原子的最小动能,与给出的原子的动能比较即可;吸收光子能量发生跃迁,吸收的光子能量需等于两能级间的能级差;根据电子的碰撞,光子可以获取10.2eV能量,从而发生跃迁.
解答 解:AB、要使运动氢原子的速度最小,则必须使二氢原子发生正碰时氢原子发生完全非弹性碰撞损失的动能将全部被基态氢原子所吸收,
由玻尔理论知二基态氢原子碰撞时损失的动能的最小值必为氢原子从n=1激发到n=2能级的能量差为:
△E=E2-E1=(-3.4)-(-13.6)=10.2eV…①
设碰前运动的氢原子最小速度为v0,初动能为Ek,碰后二氢原子速度为v,
由动量守恒得mv0=2mv…②
由能量守恒得:$\frac{1}{2}$m${v}_{0}^{2}$=$\frac{1}{2}$•2mv2+△E…③
$\frac{1}{2}$m${v}_{0}^{2}$=E0…④
代入数据得:E0=20.4eV>13.6eV
所以不能使基态氢原子发生能级跃迁,故A错误,B正确;
CD、吸收光子能量发生跃迁,吸收的光子能量需等于两能级间的能级差,即:
△E=E2-E1=(-3.4)-(-13.6)=10.2eV,
因此用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子不能跃迁到其他轨道上去,故C错误,D正确;
E、当用动能为12.3eV的电子去射向一群处于基态的氢原子,氢原子受电子照射后,原子可能吸收10.2eV的能量,从而使得原子能跃迁到n=2能级的轨道上去,故E正确;
故选:BDE.
点评 解决本题的关键知道能级差与吸收或辐射光子能量的关系,即Em-En=hv.并掌握碰撞中的动量守恒定律与能量守恒,注意用光子照射与电子碰撞,产生的不同情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.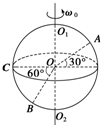 如图所示A、B、C分别是地球表面上北纬30°、南纬60°和赤道上的点.若已知地球半径为R,自转的角速度为ω0,A、B、C三点的向心加速度大小之比为( )
如图所示A、B、C分别是地球表面上北纬30°、南纬60°和赤道上的点.若已知地球半径为R,自转的角速度为ω0,A、B、C三点的向心加速度大小之比为( )
 如图所示A、B、C分别是地球表面上北纬30°、南纬60°和赤道上的点.若已知地球半径为R,自转的角速度为ω0,A、B、C三点的向心加速度大小之比为( )
如图所示A、B、C分别是地球表面上北纬30°、南纬60°和赤道上的点.若已知地球半径为R,自转的角速度为ω0,A、B、C三点的向心加速度大小之比为( )| A. | 1:1:1 | B. | 1:1:2 | C. | $\sqrt{3}$:1:2 | D. | 1:$\sqrt{3}$:2 |
2.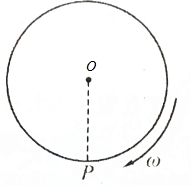 半径为R的大圆盘以角速度ω绕竖直轴顺时针方向在水平面里匀速转动,如图所示,位于圆盘边缘P点处人想开击中中心转轴上的靶标,若子弹射离枪口的水平速度为v0,则( )
半径为R的大圆盘以角速度ω绕竖直轴顺时针方向在水平面里匀速转动,如图所示,位于圆盘边缘P点处人想开击中中心转轴上的靶标,若子弹射离枪口的水平速度为v0,则( )
 半径为R的大圆盘以角速度ω绕竖直轴顺时针方向在水平面里匀速转动,如图所示,位于圆盘边缘P点处人想开击中中心转轴上的靶标,若子弹射离枪口的水平速度为v0,则( )
半径为R的大圆盘以角速度ω绕竖直轴顺时针方向在水平面里匀速转动,如图所示,位于圆盘边缘P点处人想开击中中心转轴上的靶标,若子弹射离枪口的水平速度为v0,则( )| A. | 枪应瞄准转动轴射击 | B. | 应朝PO偏右θ角射击,cosθ=$\frac{ωR}{{v}_{0}}$ | ||
| C. | 应朝PO偏右θ角射击,tanθ=$\frac{ωR}{{v}_{0}}$ | D. | 应朝PO偏右θ角射击,sinθ=$\frac{ωR}{{v}_{0}}$ |
14.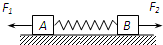 如图所示,两物体A、B用轻质弹簧相连静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在运动过程中,对A、B两物体及弹簧组成的系统,正确的说法是(整个过程中弹簧不超过其弹性限度)( )
如图所示,两物体A、B用轻质弹簧相连静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在运动过程中,对A、B两物体及弹簧组成的系统,正确的说法是(整个过程中弹簧不超过其弹性限度)( )
 如图所示,两物体A、B用轻质弹簧相连静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在运动过程中,对A、B两物体及弹簧组成的系统,正确的说法是(整个过程中弹簧不超过其弹性限度)( )
如图所示,两物体A、B用轻质弹簧相连静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在运动过程中,对A、B两物体及弹簧组成的系统,正确的说法是(整个过程中弹簧不超过其弹性限度)( )| A. | 机械能守恒 | |
| B. | 机械能不守恒 | |
| C. | 当弹簧伸长到最长时,系统的机械能最大 | |
| D. | 当弹簧弹力的大小与F1、F2的大小相等时,A、B两物体速度最大,系统机械能最大 |
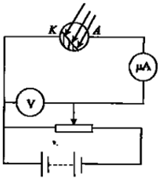 光电效应实验中,如图所示用频率为7.5×1014Hz的光照射金属K,当电压表示数减为0.91V时,灵敏电流表上才有电流出现.(普朗克常量h=6.63×10-34J•s,电子的电量为1.6×10-19C)
光电效应实验中,如图所示用频率为7.5×1014Hz的光照射金属K,当电压表示数减为0.91V时,灵敏电流表上才有电流出现.(普朗克常量h=6.63×10-34J•s,电子的电量为1.6×10-19C)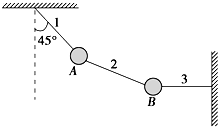 如图所示,用三条完全相同的轻质细绳1,2,3将A,B两个质量均为m的完全相同的小球连接并悬挂,小球处于静止状态,轻绳1与竖直方向的夹角为45°,轻绳3水平,求轻质细绳上1,2,3的拉力分别为多大?
如图所示,用三条完全相同的轻质细绳1,2,3将A,B两个质量均为m的完全相同的小球连接并悬挂,小球处于静止状态,轻绳1与竖直方向的夹角为45°,轻绳3水平,求轻质细绳上1,2,3的拉力分别为多大? 2008年9月27日,“神舟七号”宇航员翟志刚出舱太空行走已试验成功,如图所示,若已知地球半径为R,地球表面重力加速度为g,“神舟七号”载人飞船上的宇航员离开飞船后身上的速度计显示其对地心的速度为v,从翟志刚打开舱门开始太空行走到结束所用的时间为t,求:
2008年9月27日,“神舟七号”宇航员翟志刚出舱太空行走已试验成功,如图所示,若已知地球半径为R,地球表面重力加速度为g,“神舟七号”载人飞船上的宇航员离开飞船后身上的速度计显示其对地心的速度为v,从翟志刚打开舱门开始太空行走到结束所用的时间为t,求: