题目内容
9.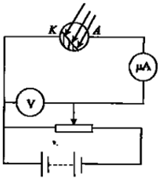 光电效应实验中,如图所示用频率为7.5×1014Hz的光照射金属K,当电压表示数减为0.91V时,灵敏电流表上才有电流出现.(普朗克常量h=6.63×10-34J•s,电子的电量为1.6×10-19C)
光电效应实验中,如图所示用频率为7.5×1014Hz的光照射金属K,当电压表示数减为0.91V时,灵敏电流表上才有电流出现.(普朗克常量h=6.63×10-34J•s,电子的电量为1.6×10-19C)(1)求该金属的逸出功;
(2)若将电路中电源正负极对调,调节滑动变阻器滑片,使电压表的示数为2V时,光电子到达阳极A的最大动能为多少?
(3)若电流表示数为0.48μA,则每秒从阴极K发射出的电子个数是多少?
分析 (1)根据光电效应方程$\frac{1}{2}$m${v}_{0m}^{2}$=hγ-W0,结合Ekm=eU0,即可求解金属的逸出功;
(2)根据光电效应方程$\frac{1}{2}$m${v}_{0m}^{2}$=hγ-W0,并依据动能定理,即可求解到达阳极A的最大动能;
(3)根据电流I=$\frac{q}{t}$,结合N=$\frac{q}{e}$,即可求解.
解答 解:(1)根据光电效应方程有:$\frac{1}{2}$m${v}_{0m}^{2}$=hγ-W0;
且Ekm=eU0,则有:eU0=hγ-W0;
解得:W0=hγ-eU0=6.63×10-34×7.5×1014-1.6×10-19×0.91=3.51×10-19J
(2)电源正负极对调,电压表的示数为2V时,设光电子到达阳极A的最大动能为:Ekm′=$\frac{1}{2}$m${v}_{0m}^{2}$+qU=hγ-W0+qU
代入数据解得:Ekm′=6.63×10-34×7.5×1014-3.51×10-19+1.6×10-19×2J=4.66×10-19J
(3)电流表示数为0.48μA,则每秒从阴极K发射出的电子个数是:
N=$\frac{q}{e}$=$\frac{It}{e}$=$\frac{0.48×1{0}^{-6}×1}{1.6×1{0}^{-19}}$=3×1012个;
答:(1)该金属的逸出功3.51×10-19J;
(2)若将电路中电源正负极对调,调节滑动变阻器滑片,使电压表的示数为2V时,光电子到达阳极A的最大动能为4.66×10-19J;
(3)若电流表示数为0.48μA,则每秒从阴极K发射出的电子个数是3×1012个.
点评 考查光电效应方程的应用,理解逸出功的概念及最大初动能的含义.注意当发生光电效应时,入射光的频率越高,而金属的逸出功是一定,则光电子的最大初动能越大.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | 平抛过程最大 | B. | 竖直上抛过程最大 | ||
| C. | 竖直下抛过程最大 | D. | 三者一样大 |
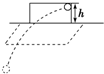 如图所示在足球赛中,红队球员在白队禁区附近主罚定位球,并将球从球门右上角贴着球门射入,球门高度为h,足球飞入球门的速度为v,足球质量为m,则红队球员将足球踢出时对足球做的功W为(不计空气阻力、足球可视为质点)( )
如图所示在足球赛中,红队球员在白队禁区附近主罚定位球,并将球从球门右上角贴着球门射入,球门高度为h,足球飞入球门的速度为v,足球质量为m,则红队球员将足球踢出时对足球做的功W为(不计空气阻力、足球可视为质点)( )| A. | $\frac{m{v}^{2}}{2}$ | B. | mgh | C. | mgh+$\frac{m{v}^{2}}{2}$ | D. | $\frac{m{v}^{2}}{2}$-mgh |
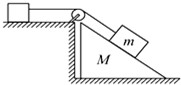 如图所示,物体m通过定滑轮牵引另一水平面上的物体沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平地面对斜面体( )
如图所示,物体m通过定滑轮牵引另一水平面上的物体沿斜面匀速下滑,此过程中斜面仍静止,斜面质量为M,则水平地面对斜面体( )| A. | 无摩擦力 | B. | 有水平向右的摩擦力 | ||
| C. | 支持力为(M+m)g | D. | 支持力大于(M+m)g |
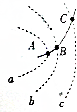 如图所示,虚线a、b、c分别代表某电场中的三条等势线,相邻等势线之间的电势差相等,一带正电粒子只在电场力作用下沿实线从A点运动到C点,B为运动轨迹上的点,则下列说法正确的是( )
如图所示,虚线a、b、c分别代表某电场中的三条等势线,相邻等势线之间的电势差相等,一带正电粒子只在电场力作用下沿实线从A点运动到C点,B为运动轨迹上的点,则下列说法正确的是( )| A. | 三个等势线中,a的电势最高 | |
| B. | 粒子从A点运动到B点电场力所做的功小于从B点运动到C点电场力所做的功 | |
| C. | A点的电场强度大小等于C点的电场强度大小 | |
| D. | 粒子在A点的电视能小于在C点的电势能 |
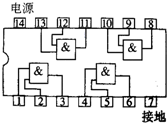 如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )
如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )| A. | 1 0 | B. | 0 1 | C. | 1 1 | D. | 0 0 |
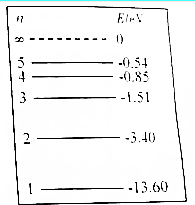 已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)
已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)