题目内容
15.图(甲)为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量Φ随时间t按图(乙)所示正弦规律变化.求: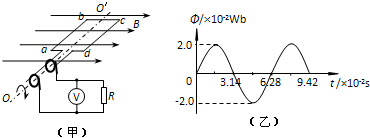
(1)交流发电机产生的电动势的表达式;
(2)电路中交流电压表的示数;
(3)从甲图所示时刻开始,线圈转过90°过程中通过线圈导线横截面的电荷量.
分析 (1)根据电动势最大值的表达式,结合磁通量的最大值,求出电动势的最大值;从而得出表达式;
(2)由欧姆定律可求得电压表的示数;
(3)根据法拉第电磁感应定律,结合磁通量的变化量求出通过电阻R的电量.
解答 解:(1)交流发电机产生电动势的最大值Em=nBSω,
因为磁通量的最大值Φm=BS=2×10-2Wb,
$ω=\frac{2π}{T}=\frac{2π}{6.28×1{0}^{-2}}=100rad/s$,
则电动势的最大值${E}_{m}=nBSω=100×2×1{0}^{-2}×100$V=200V;
故表达式e=200cos100t
(2)电动势的有效值 E=$\frac{\sqrt{2}}{2}$Em=100$\sqrt{2}$ V
由闭合电路的欧姆定律,电路中电流的有效值为I=$\frac{E}{r+R}$=$\frac{100\sqrt{2}}{10+90}$=$\sqrt{2}$A
交流电压表的示数为U=I R=90$\sqrt{2}$V=127 V;
(3)由法拉第电磁感应定律可知:$\overline{E}$=$n\frac{△Φ}{△t}$
$\overline{I}$=$\frac{\overline{E}}{{R}_{总}}$
电量q=$\overline{I}t$
解得:$q=n\frac{△Φ}{{R}_{总}}$,
q=$100×\frac{2×1{0}^{-2}}{90+10}C=0.02C$.
答(1)交流发电机产生的电动势的表达式e=200cos100t
(2)电路中交流电压表的示数为127V;
(3)从甲图所示时刻开始,线圈转过90°过程中通过线圈导线横截面的电荷量为0.02C
点评 解决本题的关键知道正弦式交流电峰值的表达式Em=nBSω,以及知道峰值、有效值、平均值和瞬时值的区别.掌握电量的表达式,并能灵活运用.

| A. | 卢瑟福的α粒子散射实验说明了原子的核式结构模型 | |
| B. | 玻尔在研究原子结构中引进了量子化的观念,并指出氢原子从低能级跃迁到高能级要吸收光子 | |
| C. | 若使放射性物质的温度升高,其半衰期将不变 | |
| D. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和10次β衰变 |
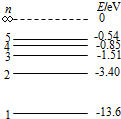
| A. | 氢原子可以辐射出连续的各种波长的光 | |
| B. | 氢原子可辐射出10种不同波长的光 | |
| C. | 氢原子从n=4的能级向n=3的能级跃迁时辐射光的波长最短 | |
| D. | 辐射光中,光子能量为0.31eV的光波长最长 | |
| E. | 用光子能量为14.2eV的光照射基态的氢原子,能够使其电离 |
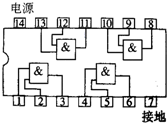 如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )
如图所示,为一个由四个“与”门组成的集成块的外引线图,现第6脚输出信号为“1”,则第4、5脚输入的信号分别为( )| A. | 1 0 | B. | 0 1 | C. | 1 1 | D. | 0 0 |
| A. | 卫星不受地球引力作用 | |
| B. | 卫星的公转周期与地球自传周期相同 | |
| C. | 卫星处于平衡状态 | |
| D. | 卫星的线速度大于第一宇宙速度 |
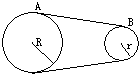
| A. | 大轮边缘的线速度小于小轮边缘的线速度 | |
| B. | 大轮的角速度大于小轮的角速度 | |
| C. | 大轮的转速等于小轮的转速 | |
| D. | 大轮边缘某点的加速度小于小轮边缘某的加速度 |
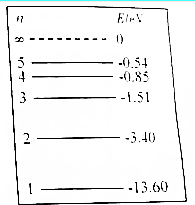 已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)
已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE(填正确答案标号)