题目内容
2．
半径为R的大圆盘以角速度ω绕竖直轴顺时针方向在水平面里匀速转动，如图所示，位于圆盘边缘P点处人想开击中中心转轴上的靶标，若子弹射离枪口的水平速度为v0，则（ ）| A． | 枪应瞄准转动轴射击 | B． | 应朝PO偏右θ角射击，cosθ=$\frac{ωR}{{v}_{0}}$ | ||
| C． | 应朝PO偏右θ角射击，tanθ=$\frac{ωR}{{v}_{0}}$ | D． | 应朝PO偏右θ角射击，sinθ=$\frac{ωR}{{v}_{0}}$ |
分析 子弹参与了两个方向上的运动，沿枪口方向上的运动和沿圆盘切线方向上的运动，当合速度的方向指向目标O时，击中目标．根据平行四边形定则进行分析．
解答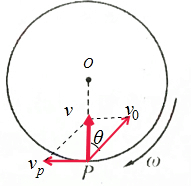 
解：射出的子弹实际上是参与了两个运动，一是沿枪口方向上的运动，一是沿P点切线方向上的运动，合运动沿PO的方向，因圆盘顺时针方向转动，所以应朝PO偏右θ角射击，如图所示．
P点此时的线速度为：vp=ωR
由几何关系有：sinθ=$\frac{{v}_{p}}{{v}_{0}}$=$\frac{ωR}{{v}_{0}}$
所以选项D正确，ABC错误．
故选：D
点评 解决本题的关键知道子弹参与两个分运动，抓住合速度的方向指向O点，运用平行四边形定则求解．解答问题时还应注意合运动的确定，实际运动时合运动，该题中的子弹的实际运动方向是沿PO的方向．
练习册系列答案
相关题目
如图所示，质量为m的木块置于斜面上，木块与斜面间的动摩擦因数为μ，在外力作用下，斜面以加速度a沿水平方向向右做匀加速运动，运动中物体m与斜面体相对静止．则木块受到的重力不做功，受到的支持力做负功，受到的摩擦力做正功（填“正功”，“负功”或“不做功”）
13．下列两个核反应构成所谓${\;}_{1}^{3}$H-${\;}_{1}^{2}$H（${\;}_{3}^{6}$Li）燃料循环，式中X、Y为生成的核或粒子，E1、E2为释放的能量：${\;}_{3}^{6}$Li+${\;}_{0}^{1}$n→X+${\;}_{2}^{4}$He+E1，${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+Y+E2，锂核、氘核和α粒子的质量分别为mLi、mD、mα，则（ ）
| A． | （mLi+mD-2mα）c2=E1+E2 | B． | （mLi+mD-mα）c2=E1+E2 | ||
| C． | 2（mLi+mD-mα）c2=E1+E2 | D． | （mLi+2mD-mα）c2=E1+E2 |
17．
如图所示，物体m通过定滑轮牵引另一水平面上的物体沿斜面匀速下滑，此过程中斜面仍静止，斜面质量为M，则水平地面对斜面体（ ）
如图所示，物体m通过定滑轮牵引另一水平面上的物体沿斜面匀速下滑，此过程中斜面仍静止，斜面质量为M，则水平地面对斜面体（ ）| A． | 无摩擦力 | B． | 有水平向右的摩擦力 | ||
| C． | 支持力为（M+m）g | D． | 支持力大于（M+m）g |
已知氢原子的能级图如图所示，则下列有关处于基态的氢原子向激发状态跃迁的说法中正确的是BDE（填正确答案标号）
2．
如图所示，电路中A、B是规格相同的灯泡，L是电阻可忽略不计的电感线圈，那么（ ）
（1）合上S，A、B一起亮，然后A变暗后熄灭
（2）合上S，B先亮，A逐渐变亮，最后A、B一样亮
（3）断开S，A立即熄灭，B由亮变暗后熄灭
（4）断开S，B立即熄灭，A闪亮一下后熄灭．
如图所示，电路中A、B是规格相同的灯泡，L是电阻可忽略不计的电感线圈，那么（ ）（1）合上S，A、B一起亮，然后A变暗后熄灭
（2）合上S，B先亮，A逐渐变亮，最后A、B一样亮
（3）断开S，A立即熄灭，B由亮变暗后熄灭
（4）断开S，B立即熄灭，A闪亮一下后熄灭．
| A． | 只有（1）正确 | B． | （1）、（3）正确 | C． | （2）、（3）、（4）正确 | D． | （1）、（4）正确 |
3．如图所为氢原子的能级图．用光子能量为13.06eV的光照射一群处于基态的氢原子，下列说法正确的是（ ）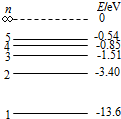
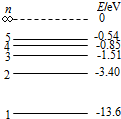
| A． | 氢原子可以辐射出连续的各种波长的光 | |
| B． | 氢原子可辐射出10种不同波长的光 | |
| C． | 氢原子从n=4的能级向n=3的能级跃迁时辐射光的波长最短 | |
| D． | 辐射光中，光子能量为0.31eV的光波长最长 | |
| E． | 用光子能量为14.2eV的光照射基态的氢原子，能够使其电离 |