题目内容
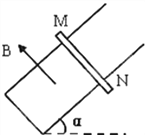
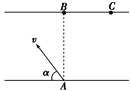
【题目】一小船从河岸的A点出发渡河，小船保持与河岸垂直方向航行，经过10min到达河对岸B点下游120m的C处，如图所示。如果小船保持原来的速度逆水斜向上游与河岸成α角方向航行，则经过12.5min恰好到达正对岸的B处。求：
(1)水流速度；
(2)α角的度数；
(3)河的宽度。
【答案】(1)0.2m/s (2)53° (3)200m
【解析】
将小船的运动分解为沿河岸方向和垂直于河岸方向，抓住分运动与合运动具有等时性，可以求出水流速度与小艇在静水中的速度，从而可求出河的宽度．
当实际航线与河岸垂直，则合速度的方向垂直于河岸，根据平行四边形定则求出船头与河岸所成的夹角．
（1）设水流速度为v1，小艇在静水中速度为v2，
艇身与河岸垂直时，
，则有
；
（2）艇身逆向上游行驶时，速度情况如图所示，
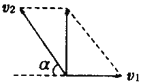
则
，艇身与河岸垂直时，
，故得
；
船头与河岸夹角
，得
；
（3）河宽
．
【题目】（1）实验小组用如图所示的装置“探究功与物体速度变化的关系”，某同学分别取1条、2条、3条…同样的橡皮筋进行第1次、第2次、第3次…实验，每次每根橡皮筋拉伸的长度都保持一致，则每次橡皮筋对小车做的功记作W0、2W0、3W0…，下列说法正确的是_____________
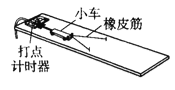
A．为减小实验误差，长木板应水平放置 |
B．通过增加橡皮筋的条数可以使橡皮筋对小车做的功成整数倍增加 |
C．小车在橡皮筋拉力作用下做匀加速直线运动，当橡皮筋恢复原长后小车做匀速运动 |
D．应选择纸带上点距均匀的一段计算小车的速度 |
（2）某同学把每次橡皮筋对小车做的功记作W0、2W0、3W0……，对每次打出的纸带进行处理，获得v，v2的数值记录在表格中。
W | 0 | W0 | 2W0 | 3W0 | 4W0 | 5W0 | 6W0 |
v/(m·s－1) | 0 | 1.0 | 1.4 | 1.7 | 2.0 | 2.2 | 2.4 |
v2/（m2·s－2） | 0 | 1 | 1.9 |
请你根据表中的数据作出W－v、W－v2图线。
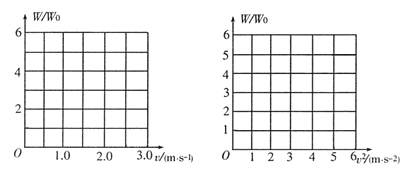
由图线探究功与物体速度变化的关系是 。
