题目内容
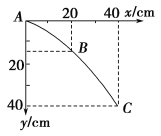
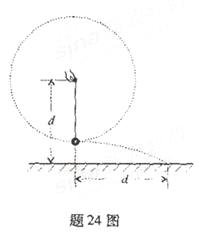
【题目】如图所示，四分之一圆弧AB和半圆弧BC组成的光滑轨道固定在竖直平面内，A、C两端点等高，直径BC竖直，圆弧AB的半径为R，圆孤BC的半径为
。一质量为m的小球从A点上方的D点由静止释放，恰好沿A点切线方向进入并沿轨道运动，不计空气阻力，重力加速度大小为g。
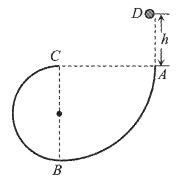
(1)要使小球能运动到C点，D、A两点间的高度差h至少为多大?
(2)改变h，小球通过C点后落到圆弧AB上的最小动能为多少
【答案】（1）
（2）
【解析】
（1）小球刚好通过C点，则重力充当向心力，结合机械能守恒定律求解h；（2）小球从C点做平抛运动，结合平抛运动的规律和机械能守恒定律找到Ek和h的函数关系，根据数学知识讨论.
（1）设小球刚好通过C点的速度为v，则mg=m
小球从D点到C点的过程中机械能守恒，有：mgh=
mv2
联立解得h=R/4
（2）设小球通过C点的速度为v0，落到圆弧AB上时，水平位移为x,下落高度为y，由平抛运动的规律可知x=v0t; y=gt2
从C点抛出到落到圆弧AB上，由动能定理
又x2+y2=R2
联立可得：
式中当
即
时，Ek有最小值，
联立可得
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
