题目内容
【题目】晓明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动,当球某次运动到最低点时,绳突然断掉。球飞离水平距离d后落地,如题24图所示,已知握绳的手离地面高度为d,手与球之间的绳长为![]() ,重力加速度为g忽略手的运动半径和空气阻力。
,重力加速度为g忽略手的运动半径和空气阻力。
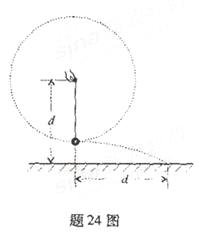
(1) 求绳断时球的速度大小v1,和球落地时的速度大小v2
(2) 问绳能承受的最大拉力多大?
(3) 改变绳长,使球重复上述运动。若绳仍在球运动到最低点时断掉,要使球抛出的水平距离最大,绳长应为多少?最大水平距离为多少?
【答案】解:
(1)v1=![]() v2=
v2=![]()
(2)T=![]() mg
mg
(3) 当l=![]() 时,x有极大值xmax=
时,x有极大值xmax=![]() d
d
【解析】
试题
(1)设绳断后球飞行时间为t,由平抛运动规律,有: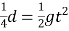 ,所以
,所以![]() 。根据机械能守恒定律则:
。根据机械能守恒定律则:![]() ,所以
,所以![]()
(2)设绳能承受的最大拉力大小为F,这也是球受到绳的最大拉力大小.球做圆周运动的半径为![]() ,根据圆周运动向心力公式
,根据圆周运动向心力公式![]() ,解得
,解得![]() 。
。
(3)设绳长为l,绳断时球的速度大小为v3,绳承受的最大拉力不变,有
![]() 得
得![]()
绳断后球做平抛运动,竖直位移为![]() ,水平位移为x,时间为
,水平位移为x,时间为![]() ,有
,有
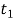
得![]() ,根据一元二次方程的特点,当
,根据一元二次方程的特点,当![]() 时,x有极大值,
时,x有极大值,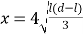

 阅读快车系列答案
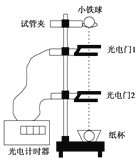
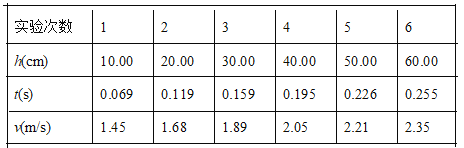
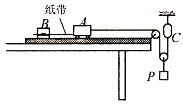
阅读快车系列答案【题目】某同学用如图所示的装置探究小车加速度与合外力的关系。图中小车A左端连接一纸带并穿过打点计时器B的限位孔,右端用一轻绳绕过滑轮系于拉力传感器C的下端,A、B置于水平放置的一端带有定滑轮的足够长的木板上。不计绳与滑轮的摩擦及滑轮的质量。实验时,先接通电源再释放小车,打点计时器在纸带上打下一系列点。该同学在保证小车A质量不变的情况下,通过改变P的质量来改变小车A所受的外力,由传感器和纸带测得的拉力F和加速度a数据如下表所示。
次数 | 1 | 2 | 3 | 4 | 5 |
F/N | 0.10 | 0.18 | 0.26 | 0.30 | 0.40 |
a/(m·s)-2 | 0.08 | 0.22 | 0.37 | __▲__ | 0.59 |
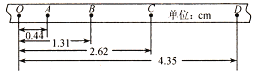
(1)第4次实验得到的纸带如图所示,O、A、B、C和D是纸带上的五个计数点,每两个相邻点间有四个点没有画出,A、B、C、D四点到O点的距离如图所示。打点计时器电源频率为50Hz。根据纸带上数据计算出加速度为___m/s2。
(2)在实验中,___(选填“需要”或“不需要”)满足重物P的质量远小于小车的质量。
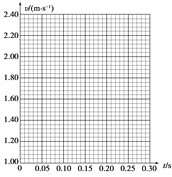
(3)根据表中数据,在图示坐标系中作出小车加速度a与力F的关系图象。
(____________)
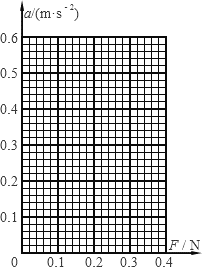
(4)根据图象推测,实验操作中重要的疏漏是__________________。