题目内容
电磁炉专用平底锅的锅底和锅壁均由耐高温绝缘材料制成,起加热作用的是安装在锅

底平面的一系列粗细均匀半径不同的同心导体环(导体环的分布如图所示),导体环所用材料每米的电阻值为R0Ω,从中心向外第n个同心圆环的半径为rn=nr0 (其中n=1,2,3,…,8,共有8个圆环,r0为已知量),如图所示。当电磁炉开启后,能产生垂直于锅底方向的变化磁场,该磁场在环状导体上产生的感应电动势规律为:e=S·2 sinωt(式中:e为瞬时感应电动势,S为环状导体所包围的圆平面的面积,ω为已知常数),那么,当电磁炉正常工作时,求:
sinωt(式中:e为瞬时感应电动势,S为环状导体所包围的圆平面的面积,ω为已知常数),那么,当电磁炉正常工作时,求:
(1)第n个导体环中感应电流的有效值表达式;
(2)前三条(靠近中心的三条)导体环释放的总功率有多大?
(3)假设导体环产生的热量全部以波长为λ的红外线光子辐射出来,
那么第三条导体环上t秒钟内射出的光子数是多少?
(光速c和普朗克常数h为已知量,t>> 2π/ω)

底平面的一系列粗细均匀半径不同的同心导体环(导体环的分布如图所示),导体环所用材料每米的电阻值为R0Ω,从中心向外第n个同心圆环的半径为rn=nr0 (其中n=1,2,3,…,8,共有8个圆环,r0为已知量),如图所示。当电磁炉开启后,能产生垂直于锅底方向的变化磁场,该磁场在环状导体上产生的感应电动势规律为:e=S·2
 sinωt(式中:e为瞬时感应电动势,S为环状导体所包围的圆平面的面积,ω为已知常数),那么,当电磁炉正常工作时,求:
sinωt(式中:e为瞬时感应电动势,S为环状导体所包围的圆平面的面积,ω为已知常数),那么,当电磁炉正常工作时,求:(1)第n个导体环中感应电流的有效值表达式;
(2)前三条(靠近中心的三条)导体环释放的总功率有多大?
(3)假设导体环产生的热量全部以波长为λ的红外线光子辐射出来,
那么第三条导体环上t秒钟内射出的光子数是多少?
(光速c和普朗克常数h为已知量,t>> 2π/ω)
(1)rn/R0= n (n=1,2,…,8) (2)72πr30/R0 (3)N3=
n (n=1,2,…,8) (2)72πr30/R0 (3)N3=
 n (n=1,2,…,8) (2)72πr30/R0 (3)N3=
n (n=1,2,…,8) (2)72πr30/R0 (3)N3=
(1)根据法拉第电磁感应定律:
第n个环中的感应电动势最大值为:Enmax=2 r2n……………………….(1分)
r2n……………………….(1分)
第n个环的电阻为:Rn=2πrn·R0……………………………………….(1分)
因此第n个环中电流的最大值为:Inmax=Enmax/Rn= rn/R0……………..(2分)
rn/R0……………..(2分)
因此第n个环中电流的有效值为:
In= =rn/R0=
=rn/R0= n (n=1,2,…,8).……………………………….(2分)
n (n=1,2,…,8).……………………………….(2分)
(2)由:P1=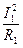 ……………………………………………………………………………..(2分)
……………………………………………………………………………..(2分)
和:Pn=I2nRn=n3P1………………………………………………………………....(2分)
前三个导电圆环,释放的总功率:
P=P1+P2+P3=(13+23+33)P1=72πr30/R0…………………………………………..(2分)
(3)设:t秒内辐射出的光子数为Nn,因为电能全部转化为光能:
∴I2nRnt=Nn·h …………………………………………………………………….(2分)
…………………………………………………………………….(2分)
c=λ …………………………………………………………………………….(2分)
…………………………………………………………………………….(2分)
∴Nn= n3………………………………………………………………………(1分)
n3………………………………………………………………………(1分)
第三条导体环上释放的光子数:N3= …………………………………………………(1分)
…………………………………………………(1分)
第n个环中的感应电动势最大值为:Enmax=2
 r2n……………………….(1分)
r2n……………………….(1分)第n个环的电阻为:Rn=2πrn·R0……………………………………….(1分)
因此第n个环中电流的最大值为:Inmax=Enmax/Rn=
 rn/R0……………..(2分)
rn/R0……………..(2分)因此第n个环中电流的有效值为:
In=
 =rn/R0=
=rn/R0= n (n=1,2,…,8).……………………………….(2分)
n (n=1,2,…,8).……………………………….(2分)(2)由:P1=
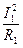 ……………………………………………………………………………..(2分)
……………………………………………………………………………..(2分)和:Pn=I2nRn=n3P1………………………………………………………………....(2分)
前三个导电圆环,释放的总功率:
P=P1+P2+P3=(13+23+33)P1=72πr30/R0…………………………………………..(2分)
(3)设:t秒内辐射出的光子数为Nn,因为电能全部转化为光能:
∴I2nRnt=Nn·h
 …………………………………………………………………….(2分)
…………………………………………………………………….(2分)c=λ
 …………………………………………………………………………….(2分)
…………………………………………………………………………….(2分)∴Nn=
 n3………………………………………………………………………(1分)
n3………………………………………………………………………(1分)第三条导体环上释放的光子数:N3=
 …………………………………………………(1分)
…………………………………………………(1分)
练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目



 匀速转动,金属棒的P端与圆环无摩擦紧密接触,整个装置放在竖直向下的匀强磁场中。已知圆环半径OP =" 20" cm,圆环总电阻为R1 = 0.4
匀速转动,金属棒的P端与圆环无摩擦紧密接触,整个装置放在竖直向下的匀强磁场中。已知圆环半径OP =" 20" cm,圆环总电阻为R1 = 0.4 ,金属棒的电阻R2 = 0.1
,金属棒的电阻R2 = 0.1







