题目内容
一行星绕恒星作圆周运动。由天文观测可得,其运动周期为T,速度为v,引力常量为G,则
A.恒星的质量为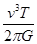 | B.行星的质量为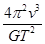 |
C.行星运动的轨道半径为 | D.行星运动的加速度为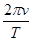 |
ACD
解析试题分析:由万有引力提供向心力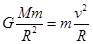 解得:
解得: ,根据公式
,根据公式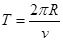 ,可得
,可得 ,联立可得:
,联立可得: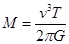 ,AC正确,由于计算过程中行星的质量相抵消,所以无法计算行星的质量,B错误;根据公式
,AC正确,由于计算过程中行星的质量相抵消,所以无法计算行星的质量,B错误;根据公式 ,
, 可得
可得 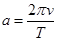 ,D正确;
,D正确;
考点:考查了万有引力定律的应用

2013年12月15日4时35分,嫦娥三号着陆器与巡视器分离,“玉兔号”巡视器顺利驶抵月球表面。如图所示是嫦娥三号奔月过程中某阶段运动的示意图,关闭动力的嫦娥三号在月球引力作用下向月球靠近,并将沿椭圆轨道在B处变轨进入圆轨道,已知嫦娥三号绕月做圆周运动轨道半径为r,周期为T,引力常量为G,下列说法正确的是
| A.图中嫦娥三号正减速飞向B处 |
| B.嫦娥三号在B处由椭圆轨道进入圆轨道必须点火减速 |
| C.根据题中条件可以算出月球质量 |
| D.根据题中条件可以算出嫦娥三号受到月球引力的大小 |
今年 12月2日1时30分,搭载着嫦娥三号的长征三号乙运载火箭在西昌卫星发射中心发射升空并准确入轨,发射圆满成功。“嫦娥三号”月球探测器在环绕月球运行过程中,设探测器运行的轨道半径为r,运行速率为v,当探测器在飞越月球上一些环形山中的质量密集区上空时
| A.r、v 都将略为减小 | B.r、v都将保持不变 |
| C.r将略为减小,v将略为增大 | D.r将略为增大,v将略为减小 |
一颗人造地球卫星,在地面时,所受万有引力大小为F;当它被送到距地心的距离为地球半径2倍的运行轨道后,所受万有引力大小为( )
A.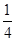 F F | B.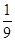 F F | C.F | D.3F |
北京时间2012年4月30日,在西昌卫星发射中心我国首次一箭双星发射中、高轨道卫星,成功将两颗北斗二号卫星送入预定圆轨道.“北斗二号”地球卫星导航系统由中轨道、高轨道和同步卫星等组成,若三种卫星质量均相等,中轨道卫星离地最近,同步卫星离地最远.关于在轨道上运行的卫星,下列说法中正确的是
| A.同步卫星的线速度最小 |
| B.中轨道卫星的动能最小 |
| C.高轨道卫星的重力势能最大 |
| D.高轨道卫星的向心加速度最大 |
目前在地球同步轨道上运行的同步卫星,下列说法中正确的是( )
| A.向心力大小相同 | B.周期相同 |
| C.向心加速度相同 | D.离地心的距离相同 |
一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后做匀速圆周运动,动能减小为原来的1/4,不考虑卫星质量的变化,则变轨前后卫星的
| A.向心加速度大小之比为4:1 | B.角速度大小之比为2:1 |
| C.周期之比为1:8 | D.轨道半径之比为1:2 |
宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统,设某双星系统绕其连线上的O点做匀速圆周运动,如图所示。若AO<OB,则( ) 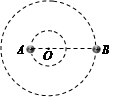
| A.星球A的向心力一定大于B的向心力 |
| B.星球A的线速度一定大于B的线速度 |
| C.星球A的角速度一定小于B的角速度 |
| D.星球A的质量一定大于B的质量 |
