题目内容
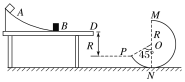
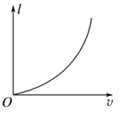
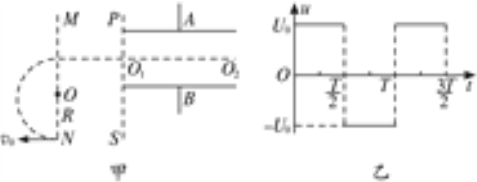
【题目】如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板.开始时质量为m=1 kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平面上运动的v-t图像如图乙所示,g=10 m/s2.求:
(1)水平作用力F的大小;
(2)滑块开始下滑时的高度;
(3)木板的质量.
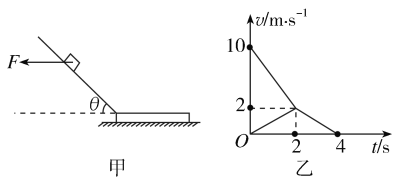
【答案】(1) ![]() N (2)2.5 m (3)1.5 kg
N (2)2.5 m (3)1.5 kg
【解析】
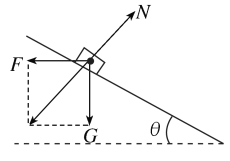
(1)滑块受到水平推力F、重力mg和支持力N处于平衡,如图所示:
mgsinθ=Fcosθ
代入数据可得F=![]() N
N
(2)由题意可知,滑块滑到木板上的初速度为10 m/s
当F变为水平向右之后,由牛顿第二定律可得
mgsinθ+Fcosθ=ma
解得a=10 m/s2
下滑的位移:x=![]()
解得x=5 m
故下滑的高度:h=xsin30°=2.5 m
(3)由图像可知,二者先发生相对滑动,当达到共速后一块做匀减速运动,设木板与地面间的动摩擦因数为μ1,滑块与木板间的动摩擦因数为μ2
二者共同减速时的加速度大小a1=1 m/s2,发生相对滑动时,木板的加速度a2=1 m/s2,滑块减速的加速度大小为:a3=4 m/s2
对整体受力分析,可得a1=![]() =μ1g
=μ1g
可得μ1=0.1
在0~2 s内分别对m和M做受力分析可得
对M:μ2mg-μ1(M+m)g=Ma2
对m:μ2mg=ma3
带入数据解方程可得M=1.5 kg

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目