��Ŀ����
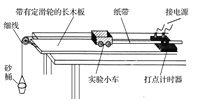
����Ŀ����ͼ��ʾ��ˮƽ���������һ���˸�Ϊh�Ĺ⻬Բ���ι����Բ���ĵ���������ͬһˮƽ����.�����Ҳ���һ��ֱ���õĹ⻬Բ���MNP������״Ϊ�뾶R��0.8m��Բ����ȥ�����Ͻ�135���ʣ��IJ��֣�MNΪ����ֱֱ����P�㵽�������ֱ����ҲΪR.һ����m��0.4kg�����A��Բ���ι���Ķ��˾�ֹ�ͷţ�����Բ���ι����ǡ��һͣ��Բ����ˮƽ����������ҲΪm�����B������������(��ײ����û�л�е�ܵ���ʧ)���������B��λ����ʱ��仯�Ĺ�ϵʽΪx��6t��2t2(��ϵʽ�������������ĵ�λ��Ϊ���ʵ�λ)�����B���������ǡ��P������������Բ���.(�������ٶ�gȡ10m/s2)��
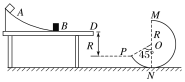
(1)BP���ˮƽ����xBP��
(2)�ж����B�ܷ���Բ�������M�㣻
(3)���A�ɾ�ֹ�ͷŵĸ߶�h.
���𰸡�(1)4.1m (2)���� (3)1.8m
��������(1)����ײ�����B��D���Գ��ٶ�vD��ƽ���˶����䵽P��ʱ����ֱ�ٶ�Ϊvy��![]()
ͬʱ![]() ��tan45�㣬���vD��4m/s
��tan45�㣬���vD��4m/s
��ƽ����ʱΪt��ˮƽλ��Ϊx������R��![]() gt2
gt2
x��vDt
���x��1.6m
���B�����Գ��ٶ�v0��6m/s�����ٶȴ�С
a����4m/s2���ٵ�vD����BD���λ��Ϊ
x1��![]() ��2.5m
��2.5m
��BP֮���ˮƽ����xBP��x��x1��4.1m
(2)�����B���ع������M�㣬��M��ʱ���ٶ�ΪvM������![]() mv
mv![]() ��
��![]() mv
mv![]() ����
����![]() mgR
mgR
����������ѹ��ΪFN����FN��mg��m![]()
���FN��(1��![]() )mg<0������鲻�ܵ���M��.
)mg<0������鲻�ܵ���M��.
(3)�����A��B����ײ���̣��У�
mAvA��mAvA�䣫mBv0
![]() mAv
mAv![]() ��
��![]() mAvA��2��
mAvA��2��![]() mBv
mBv![]()
��ã�vA��6m/s
�����A�ͷŵĸ߶�Ϊh����
mgh��![]() mv
mv![]() ��
��
���h��1.8m

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�