题目内容
【题目】一粗细均匀的J型细玻璃管竖直放置,短臂端封闭,长臂端![]() 足够长
足够长![]() 开口向上,短臂内封有一定质量的理想气体,初始状态时管内各段长度如图所标,密闭气体的温度为
开口向上,短臂内封有一定质量的理想气体,初始状态时管内各段长度如图所标,密闭气体的温度为![]() 大气压强为76cmHg,求:
大气压强为76cmHg,求:
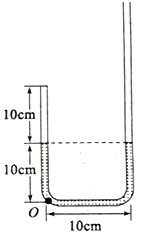
(1)若沿长臂的管壁缓慢加入水银,密闭气体长度变为8cm,注入水银柱有多长?
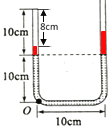
(2)在注完水银后,使玻璃管沿绕过O点的水平轴在纸面内逆时针转过![]() 稳定后,要使密闭气体的长度保持8cm不变,应使气体温度变为多少?
稳定后,要使密闭气体的长度保持8cm不变,应使气体温度变为多少?![]() 结果保留三位有效数字
结果保留三位有效数字![]()
【答案】(1) 23cm (2) 208K
【解析】
![]() 若沿长臂的管壁缓慢加入水银,封闭气体发生等温变化,对封闭气体运用玻意耳定律,结合几何关系,联立即可求出要使密闭气体长度变为8cm,注入水银柱的长度;
若沿长臂的管壁缓慢加入水银,封闭气体发生等温变化,对封闭气体运用玻意耳定律,结合几何关系,联立即可求出要使密闭气体长度变为8cm,注入水银柱的长度;
![]() 分析可知在注完水银后,封闭气体的体积与最终封闭气体的气体的体积一样,对该过程封闭气体运用查理定律,即可求出末态封闭气体的最终温度。
分析可知在注完水银后,封闭气体的体积与最终封闭气体的气体的体积一样,对该过程封闭气体运用查理定律,即可求出末态封闭气体的最终温度。
![]() 设玻璃管的横截面积为S,大气压为
设玻璃管的横截面积为S,大气压为![]() ,末态两液面的高度差为
,末态两液面的高度差为![]() ,
,
因为是缓慢加入水银,故封闭气柱发生等温变化,
初态:压强![]() ,体积
,体积![]()
末态:压强![]() ,体积
,体积![]()
根据玻意耳定律可得:![]()
解得末态封闭气柱的压强:![]()
对末态根据平衡可得:![]()
可得:![]()
根据几何关系可知注入水银柱的长度为:![]()
![]() 分析可知在注完水银后,封闭气体的体积与最终封闭气体的气体的体积一样,
分析可知在注完水银后,封闭气体的体积与最终封闭气体的气体的体积一样,
初态:压强![]() ,温度
,温度![]()
末态:压强![]() ,温度
,温度![]()
根据查理定律可得:![]()
解得最终气体温度:![]()

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目