��Ŀ����
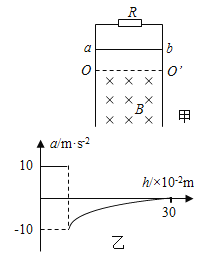
����Ŀ����ͼ����ʾ�����費���Ҽ��ΪL=1m�Ĺ⻬ƽ�н���������ֱ���ã��϶�������ֵΪR=2���ĵ��裬����OO���·��д�ֱ�ڵ���ƽ�����ڵ���ǿ�ų����ֽ�����Ϊm=0.3kg�����費�ƵĽ�����ab��OO���Ϸ�ij���ɾ�ֹ�ͷţ�����������뵼�챣�����ýӴ���ʼ��ˮƽ���ڽ�����ab����0.3m�Ĺ����У�����ٶ�a���������h�Ĺ�ϵͼ����ͼ����ʾ����֪ab����ų�ʱ���ٶ�v0=2.0m/s��ȡg=10m/s2��������˵����ȷ����
A. ����ų�������ab�е����ķ�����a��b
B. ��ǿ�ų��ĴŸ�Ӧǿ��Ϊ2.0T
C. ������ab����0.3mʱ�����ٶ�Ϊ1.0m/s
D. ������ab����0.3m�Ĺ����У�R�ϲ���������Ϊ0.75J
���𰸡�ACD
������������������������и�Ӧ�����ķ��������ֶ����жϣ�����ͼ���������˽���ų�ʱ���ٶȵĴ�С���жϳ����ٶȷ����ɷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ�����Ƶ������������ٶȵĹ�ϵʽ����ţ�ٵڶ�������ʽ������Ÿ�Ӧǿ�ȣ���ͼ����������0.3mʱ�������˵ļ��ٶ�Ϊ�㣬������ֱ���˶��������밲����ƽ�⣬��ʽ������˵��ٶȣ��ӿ�ʼ���䵽����0.3m�Ĺ����У��˵Ļ�е�ܼ�Сת��Ϊ���ܣ��������غ���ʽ���������R�ϲ�����������
����ų��������ֶ����жϿ�֪������ab�е����ķ�����a��b����A��ȷ������ͼ֪���ս���ų�ʱ�������˵ļ��ٶȴ�С![]() ��������ֱ���ϣ���ţ�ٵڶ����ɵã�
��������ֱ���ϣ���ţ�ٵڶ����ɵã� ![]() ����˸ս���ų�ʱ���ٶ�Ϊ
����˸ս���ų�ʱ���ٶ�Ϊ![]() ������
������![]() ��������
��������![]() ������ã�
������ã� ![]() ����B��������ʱ��ͨ��a-hͼ��֪a=0�������������ܵ��������밲����ƽ����
����B��������ʱ��ͨ��a-hͼ��֪a=0�������������ܵ��������밲����ƽ����![]() ������
������![]() ��������
��������![]() ����C��ȷ���ӿ�ʼ������Ĺ����У����ܵ�ת�����غ㶨����
����C��ȷ���ӿ�ʼ������Ĺ����У����ܵ�ת�����غ㶨����![]() ��������ֵ��
��������ֵ��![]() ����D��ȷ��
����D��ȷ��

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�