题目内容
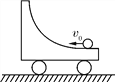
【题目】如图所示,在光滑水平面上停放着质量为m装有光滑弧形槽的小车,一个质量也为m的小球以水平速度v0沿槽口向小车滑去,到达某一高度后,小球又返回右端,则( )
A. 小球以后将向右做平抛运动
B. 小球将做自由落体运动
C. 此过程小球对小车做的功为![]()
D. 小球在弧形槽上升的最大高度为![]()
【答案】BCD
【解析】试题分析:小球和小车组成的系统在水平方向上动量守恒,当小球上升的最高点时,竖直方向上的速度为零,水平方向上与小车具有相同的速度,结合动量守恒和能量守恒求出上升的最大高度.根据动量守恒定律和能量守恒求出小球返回右端时的速度,从而得出小球的运动规律,根据动能定理得出小球对小车做功的大小.
设小球离开小车时,小球的速度为v1,小车的速度为v2,整个过程中动量守恒,得: ![]() ①,由动能守恒得
①,由动能守恒得![]() ②,联立①②得
②,联立①②得![]() ,即小球与小车分离后二者交换速度;所以小球与小车分离后做自由落体运动,A错误B正确;对小车运用动能定理得,小球对小车做功
,即小球与小车分离后二者交换速度;所以小球与小车分离后做自由落体运动,A错误B正确;对小车运用动能定理得,小球对小车做功![]() ,C正确;当小球与小车的水平速度相等时,小球弧形槽上升到最大高度,设该高度为h,则
,C正确;当小球与小车的水平速度相等时,小球弧形槽上升到最大高度,设该高度为h,则![]() ③,
③,![]() ④,联立③④解得
④,联立③④解得![]() ,D正确.
,D正确.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目