题目内容
【题目】如图甲所示,长为4m的水平轨道AB与半径为R=0.6m的竖直半圆弧轨道BC在B处相连接,有一质量为1kg的滑块(大小不计),从A处由静止开始受水平向右的力F作用,F的大小随位移变化关系如图乙所示,滑块与AB间动摩擦因数为0.25,与BC间的动摩擦因数未知,取g =l0m/s2。求:
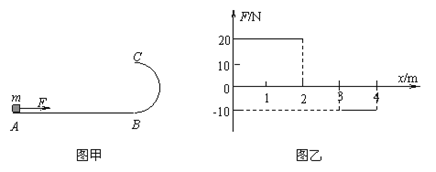
(1)滑块到达B处时的速度大小;
(2)滑块在水平轨道AB上运动前2m过程中所需的时间;
(3)若滑块到达B点时撤去力F,滑块沿半圆弧轨道内侧上滑,并恰好能达到最高点C,则滑块在半圆轨道上克服摩擦力所做的功是多少。
【答案】(1)![]() (2)
(2)![]() (3)5J
(3)5J
【解析】试题分析: (1)对滑块从A到B的过程,由动能定理得
F1x1-F3x3-μmgx=![]() mvB2得vB=2
mvB2得vB=2![]() m/s.
m/s.
(2)在前2 m内,由牛顿第二定律得
F1-μmg=ma 且x1=![]() at12
at12
解得t1=![]() s.
s.
(3)当滑块恰好能到达最高点C时,有mg=m![]()
对滑块从B到C的过程,由动能定理得
W-mg×2R=![]() mvC2-
mvC2-![]() mvB2
mvB2
代入数值得W=-5 J
即克服摩擦力做的功为5 J.

练习册系列答案
相关题目