题目内容
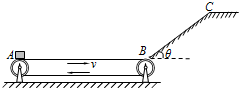用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端．传送带AB的长度L=11m，上表面保持匀速向右运行，运行的速度v=12m/s．传送带B端靠近倾角θ=37？的斜面底端，斜面底端与传送带的B端之间有一段长度可以不计的小圆弧．在A、C处各有一个机器人，A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱（可视为质点）轻放在传送带A端，货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零，C点处机器人立刻将货物箱搬走．已知斜面BC的长度s=5.0m，传送带与货物箱之间的动摩擦因数μ0=0.55，货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
，g=10m/s2（sin37°=0.6，cos37°=0.8）．求：
（1）斜面与货物箱之间的动摩擦因数μ；
（2）如果C点处的机器人操作失误，未能将第一个到达C点的货物箱搬走而造成与第二个货物箱在斜面上相撞．求两个货物箱在斜面上相撞的位置到C点的距离．（本问结果可以用根式表示）
解：
（1）货物箱在传送带上做匀加速运动过程，根据牛顿第二定律有
μ0mg=ma0
解得 a0=μ0g=5.5m/s2
由运动学公式 v12=2a0L
解得货物箱运动到传送带右端时的速度大小为
v1=11m/s＜v=12m/s，说明货物箱在传送带上一直做匀加速运动．
货物箱刚冲上斜面时的速度 v2=（1-）v1=10m/s
货物箱在斜面上向上运动过程中 v22=2a1s
解得 a1=10m/s2
根据牛顿第二定律 mgsinθ+μmgcosθ=ma1
解得 μ=0.5
（2）货物箱由A运动到B的时间为t1=
=2s，由B运动到C的时间为t2=
=1s，可见第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面．
货物箱沿斜面向下运动，根据牛顿第二定律有
mgsinθ-μmgcosθ=ma2
解得加速度大小 a2=2.0m/s2
设第一个货物箱在斜面C端沿斜面向下运动与第二个货物箱相撞的过程所用时间为t，有
v2t-
a1t 2+a2t 2=s
解得t=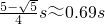
两个货物箱在斜面上相遇的位置到C端的距离
s1=a2t 2=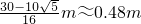
答：
（1）斜面与货物箱之间的动摩擦因数μ=0.5；
（2）如果C点处的机器人操作失误，未能将第一个到达C点的货物箱搬走而造成与第二个货物箱在斜面上相撞，两个货物箱在斜面上相撞的位置到C点的距离为0.48m．
分析：（1）货物箱在传送带上做匀加速运动过程，根据牛顿第二定律求出加速度，由速度位移关系公式求出货物箱运动到传送带右端时的速度大小，根据货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的，得到货物箱刚冲上斜面时的速度．货物箱在斜面上向上运动过程中做匀减速运动，已知初速度、末速度为零，位移为s，由速度位移关系公式求出加速度大小，由牛顿第二定律求出斜面与货物箱之间的动摩擦因数μ．
（2）由运动学公式分别求出货物箱由A运动到B的时间和由B运动到C的时间，得到第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面，然后货物箱沿斜面向下做匀加速运动，由牛顿第二定律求出加速度，当第一个货物箱与第二个货物箱相遇时，两者位移大小之和等于斜面的长度s，由位移公式求出相遇时间，再求出两个货物箱在斜面上相遇的位置到C端的距离．
点评：此题文字较多，首先要有耐心读题．对于传送带问题，关键是分析物体的运动情况，本题要边计算边分析，不能只定性分析．
（1）货物箱在传送带上做匀加速运动过程，根据牛顿第二定律有
μ0mg=ma0
解得 a0=μ0g=5.5m/s2
由运动学公式 v12=2a0L
解得货物箱运动到传送带右端时的速度大小为
v1=11m/s＜v=12m/s，说明货物箱在传送带上一直做匀加速运动．
货物箱刚冲上斜面时的速度 v2=（1-
）v1=10m/s货物箱在斜面上向上运动过程中 v22=2a1s
解得 a1=10m/s2
根据牛顿第二定律 mgsinθ+μmgcosθ=ma1
解得 μ=0.5
（2）货物箱由A运动到B的时间为t1=
=2s，由B运动到C的时间为t2==1s，可见第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面．货物箱沿斜面向下运动，根据牛顿第二定律有
mgsinθ-μmgcosθ=ma2
解得加速度大小 a2=2.0m/s2
设第一个货物箱在斜面C端沿斜面向下运动与第二个货物箱相撞的过程所用时间为t，有
v2t-
a1t 2+a2t 2=s 解得t=
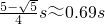
两个货物箱在斜面上相遇的位置到C端的距离
s1=
a2t 2=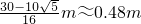答：
（1）斜面与货物箱之间的动摩擦因数μ=0.5；
（2）如果C点处的机器人操作失误，未能将第一个到达C点的货物箱搬走而造成与第二个货物箱在斜面上相撞，两个货物箱在斜面上相撞的位置到C点的距离为0.48m．
分析：（1）货物箱在传送带上做匀加速运动过程，根据牛顿第二定律求出加速度，由速度位移关系公式求出货物箱运动到传送带右端时的速度大小，根据货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
，得到货物箱刚冲上斜面时的速度．货物箱在斜面上向上运动过程中做匀减速运动，已知初速度、末速度为零，位移为s，由速度位移关系公式求出加速度大小，由牛顿第二定律求出斜面与货物箱之间的动摩擦因数μ．（2）由运动学公式分别求出货物箱由A运动到B的时间和由B运动到C的时间，得到第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面，然后货物箱沿斜面向下做匀加速运动，由牛顿第二定律求出加速度，当第一个货物箱与第二个货物箱相遇时，两者位移大小之和等于斜面的长度s，由位移公式求出相遇时间，再求出两个货物箱在斜面上相遇的位置到C端的距离．
点评：此题文字较多，首先要有耐心读题．对于传送带问题，关键是分析物体的运动情况，本题要边计算边分析，不能只定性分析．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，水平传送装置由半径为R=
某人用如图所示的方法传递物品．将一根长为L=8.0m的不可伸长的细绳，两端固定在相距为d=4.0m的A、B两等高点，运送物品的吊篮上方安装一只滑轮P，滑轮可在绳子上自由滑动，已知吊篮和物品的总质量为m=50kg．开始时，人用水平力拉住吊篮，使吊篮处于静止状态，此时AP绳呈竖直，AP与BP两绳之间的夹角
的主动轮O1和从动轮O2及传送带等构成。两轮轴心相距L=8.0米，轮与传送带不打滑。现用此装置运送一袋面粉，已知面粉袋与传送带间的动摩擦因数为μ=0.4，这袋面粉中间的面粉可不断地从袋中渗出。
（1）当传送带以v0==4.0m/s的速度匀速运动时，将这袋面粉由左端O2正上方的A点轻放在传送带上后，这袋面粉由A端运送到O1正上方的B端所用时间为多少？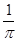
m的主动轮O1和从动轮O2及平传送带等构成，两轮轴心相距L=8m，轮与传送带不打滑，现用此装置运送一袋面粉，已知这袋面粉与传送带的动摩擦因数为
=0.4，这袋面粉中的面粉可不断地从袋中渗出。