题目内容
5. 如图所示在竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该
如图所示在竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该匀强电场中,用绝缘丝线悬挂质量为m的带正电小球,丝线跟竖直方向成θ角时小球恰
好平衡,此时小球距离右板距离为b,重力加速度为g,求:
(1)悬线对小球的拉力为多大?
(2)小球带电荷量是多少?
(3)若剪断丝线,小球碰到金属板需多长时间?
分析 (1)先分析小球的受力情况,重力竖直向下,电场力水平向右,绳子拉力沿绳子向上,处于三力平衡状态,根据平衡条件求解电荷量;
(2)如将细线剪断,绳子的拉力撤去,其余二力的合力一定沿绳子的反方向,大小等于原先绳子的力,所以小球将做匀加速直线运动,根据匀变速直线运动规律解出物体的运动时间
解答 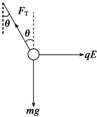 解:由于小球处于平衡状态知小球带正电,对小球受力分析如右图所示
解:由于小球处于平衡状态知小球带正电,对小球受力分析如右图所示
FTsin θ=qE①
FTcos θ=mg②
由$\frac{①}{②}$得tan θ=$\frac{qE}{mg}$,故q=$\frac{mgtanθ}{E}$,${F}_{T}=\frac{mg}{cosθ}$
(2)由第(1)问中的方程②知FT=$\frac{mg}{cosθ}$,而剪断丝线后小球所受电场力和重力的合力与未剪断丝线时丝线对小球的拉力大小相等,故剪断丝线后小球所受重力、电场力的合力等于$\frac{mg}{cosθ}$.小球的加速度a=$\frac{F合}{m}$=$\frac{g}{cosθ}$,小球由静止开始沿着丝线拉力的反方向做匀加速直线运动,当碰到金属板上时,它的位移为x=$\frac{b}{sinθ}$,又由x=$\frac{1}{2}$at2,
得t=$\sqrt{\frac{2b}{g}cotθ}$
答:(1)悬线对小球的拉力为$\frac{mg}{cosθ}$
(2)小球带电荷量是$\frac{mgtanθ}{E}$
(3)若剪断丝线,小球碰到金属板需时间为$\sqrt{\frac{2b}{g}cotθ}$
点评 解决本题的关键正确分析小球的受力情况和运动情况,知道正电荷所受的电场力方向与电场强度方向相同

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.“开普勒-452b”是天文学家确认发现首颗位于“宜居带”上体积最接近地球大小的行星,若已知它的半径R=7.6×106m,表面重力加速度g=20m/s2,G=6.7×1011N•m2/kg2,由以上已知数据不能估算出有关该行星的物理量是( )
| A. | 质量 | B. | 平均密度 | C. | 公转的周期 | D. | 第一宇宙速度 |
10.直线运动中,下列关于瞬时速度、平均速度、瞬时速率的说法中正确的是( )
| A. | 瞬时速度是物体在某一时刻或某一位置时的速度 | |
| B. | 瞬时速度是物体通过的路程及对应时间的比值 | |
| C. | 运动方向不变时,瞬时速率就是平均速度的大小 | |
| D. | 平均速度是指物体通过的路程与对应时间的比值 |
 某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.
某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.