题目内容
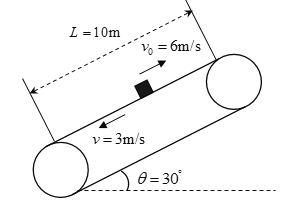
【题目】如图所示,倾角θ=30°、长度L=10m的传送带以v=3m/s的速度稳定地逆时针传动。质量m=0.5kg、底部带有红色颜料的小滑块从距传送带底端d=6.75m的P处,以v0=6m/s的初速度向上运动。已知滑块与传送带的动摩擦因数![]() 。试求:
。试求:
(1)滑块向上滑行时的加速度大小;
(2)滑块在传送带上运动的时间;
(3)滑块在传送带上留下的红色痕迹长度。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 。
。
【解析】
(1)对滑块受力
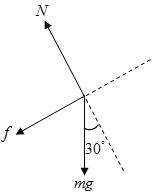
根据牛顿第二定律:
![]()
解得:![]() ;
;
(2)滑块沿传送带向上减速用时:
![]()
解得:![]()
减速过程中速度和位移关系:
![]()
解得:![]()
滑块速度减为0时:
![]()
未到达传送带顶端,之后沿传送带向下运动,加速至与传送带速度相等用时:
![]()
解得:![]()
加速度位移:
![]()
解得:![]()
滑块和传送带共速后,因为:
![]()
所以物块继续加速下滑,根据牛顿第二定律:
![]()
解得:![]()
之后滑块距离传送带底端的距离:
![]()
滑至底端:
![]()
解得:![]() (
(![]() 舍去),所以在传送带上一共用时:
舍去),所以在传送带上一共用时:
![]() ;
;
(3)根据滑块和传送带的运动情况,画出![]() 图,折线为传送带图像,横线为传送带图像:
图,折线为传送带图像,横线为传送带图像:
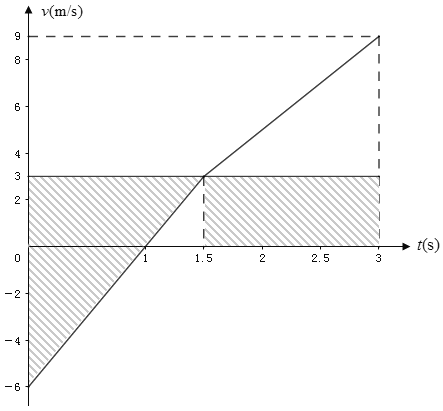
根据相对位移关系可知,图中阴影部分即为滑块在传送带上留下的红色痕迹长度:
![]() 。
。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目