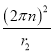Question

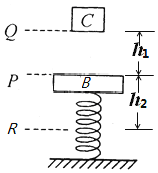
【题目】如图所示，固定在水平面上的竖直轻弹簧，上端与质量为2m的物块B相连，整个装置处于静止状态时物块B位于P处，另有一质量为m的物块C，从Q处自由下落，与B相碰撞后瞬间粘合牢固，然后一起向下运动，将弹簧进一步压缩到最低点R后，物块B、C被反弹，已知QP距离为，PR距离为，弹簧劲度系数为k，重力加速度为g，不计空气阻力，求：

（1）物块C与B相碰撞后瞬间的共同速度；

（2）弹簧压缩到最低点R时所具有的弹性势能；

（3）反弹过程中，当物块B达到最大速度时的位置到P点的距离x。

Answer 1

【答案】（1）；（2）；（3）。

【解析】

（1）由机械能守恒即可求出物块C到达P处的速度；C与B碰撞的过程中时间短，可以认为动量守恒，由此求出共同速度；（2）压缩弹簧的过程中机械能守恒，由此即可求出弹簧的弹性势能；（3）当物块B达到最大速度时，物块B与C的加速度为零，对整体进行受力分析，然后结合胡克定律即可求出。

（1）物块C从Q点下落，做自由落体运动，设到达P处时速度为，由机械能守恒：
物块C与B碰撞后粘合在一起，设两者共同速度为，
由系统动量守恒：
联立解得：；

（2）物块C与B压缩弹簧到最低点R过程，由能量守恒定律得：
原先物块B静止于弹簧，设弹簧压缩量为
由二力平衡得：
弹
反弹过程中，当物块B达到最大速度时，物块B与C的加速度为零，设此时弹簧压缩量为，有：所以物块B达到最大速度时的位置到P点的距离：