题目内容
如图所示,水平桌面上有两根相距为L=20cm,足够长的的水平平行光滑导轨,导轨的一端连接电阻R=0.9Ω,若在导轨平面上建立直角平面坐标系,取与导轨平行向右方向为x轴正方向,而与导轨垂直的水平方向为y轴方向。在x < 0的一侧没有磁场,在x > 0的一侧有竖直向下的磁场穿过导轨平面。该磁场磁感应强度的大小沿y轴方向均匀,但沿x轴方向随x的增大而增大,且B=kx,式中k=15/4T/m。质量为M的金属杆AB水平而与导轨垂直放置,可在导轨上沿与导轨平行的方向运动,当t=0时,AB位于x=0处,并有沿x轴正方向的初速度v0=5m/s。在运动过程中,有一大小变化的沿x轴方向的水平拉力F作用于AB,使AB有沿x轴负方向、大小为a=10m/s2的恒定加速度作匀变速直线运动。除R外,其它电阻均忽略不计。求:

(1)该回路中产生感应电流可以持续的时间;
(2)当AB向右运动的速度为3 m/s时,回路中的感应电动势的大小;
(3)若满足x < 0时F=0,求AB经1.6s时的位置坐标,并写出AB向右运动时拉力F与时间t的函数关系(直接用a、v0、M、k、R、L表示),以及在0.6s时金属杆AB受到的磁场力。

(1)该回路中产生感应电流可以持续的时间;
(2)当AB向右运动的速度为3 m/s时,回路中的感应电动势的大小;
(3)若满足x < 0时F=0,求AB经1.6s时的位置坐标,并写出AB向右运动时拉力F与时间t的函数关系(直接用a、v0、M、k、R、L表示),以及在0.6s时金属杆AB受到的磁场力。
(1)t=t1+t2="1s"
(2)E=B2Lv2=3×0.2×3=1.8V。
(3)①x3=-v0t3=-5×(1.6-1)="-3m"
② F+F安=Ma
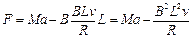

③ 方向:沿X轴正方向
方向:沿X轴正方向
(2)E=B2Lv2=3×0.2×3=1.8V。
(3)①x3=-v0t3=-5×(1.6-1)="-3m"
② F+F安=Ma
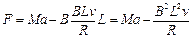

③
 方向:沿X轴正方向
方向:沿X轴正方向(1)棒减速到零所用时间 ,棒返回时间t1=t2=0.51s。
,棒返回时间t1=t2=0.51s。
有电流的时间即为棒在磁场中的运动时间,所以t=t1+t2="1s"
(2)当AB向右运动的速度为3 m/s时,杆的位移为: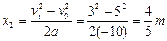 ,此时杆处的磁感强度为:
,此时杆处的磁感强度为: ,所以E=B2Lv2=3×0.2×3=1.8V。
,所以E=B2Lv2=3×0.2×3=1.8V。
(3)①由(1)可知1秒棒回到0位置,离开磁场后做匀速直线运动。
速度向左大小v3="5m/s," 得:x3=-v0t3=-5×(1.6-1)="-3m"
②

因为匀变速直线运动,所以有:F+F安=Ma
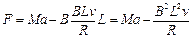

③当t=0.6s时, 而vt=v0-at=5-10×0.6="-1.0m/s " 得:
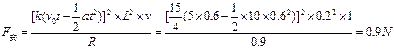 方向:沿X轴正方向
方向:沿X轴正方向
 ,棒返回时间t1=t2=0.51s。
,棒返回时间t1=t2=0.51s。有电流的时间即为棒在磁场中的运动时间,所以t=t1+t2="1s"
(2)当AB向右运动的速度为3 m/s时,杆的位移为:
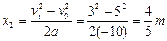 ,此时杆处的磁感强度为:
,此时杆处的磁感强度为: ,所以E=B2Lv2=3×0.2×3=1.8V。
,所以E=B2Lv2=3×0.2×3=1.8V。(3)①由(1)可知1秒棒回到0位置,离开磁场后做匀速直线运动。
速度向左大小v3="5m/s," 得:x3=-v0t3=-5×(1.6-1)="-3m"
②


因为匀变速直线运动,所以有:F+F安=Ma
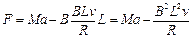

③当t=0.6s时, 而vt=v0-at=5-10×0.6="-1.0m/s " 得:
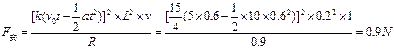 方向:沿X轴正方向
方向:沿X轴正方向
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目



 、
、 间接有阻值为
间接有阻值为 的小电珠,整个轨道处在磁感强度为
的小电珠,整个轨道处在磁感强度为 的匀强磁场中,两导轨间距为
的匀强磁场中,两导轨间距为 。现有一质量为
。现有一质量为 、电阻为
、电阻为 从
从 、
、 ,此时速度为
,此时速度为 。
。
 ,速度为v,求此时刻作用在杆上安培力的大小.
,速度为v,求此时刻作用在杆上安培力的大小.






 .被一竖直绝缘线悬吊起来的水平直导线ef的长工为L,质量为m,与线框d接触良好.ef处在一个垂直于纸面向外的匀强磁场中,磁感应强度为
.被一竖直绝缘线悬吊起来的水平直导线ef的长工为L,质量为m,与线框d接触良好.ef处在一个垂直于纸面向外的匀强磁场中,磁感应强度为 .整个装置的总电阻为R.当
.整个装置的总电阻为R.当 (变化率)为某一定值时绝缘线对ef的拉力恰好为零.在这种情况下:
(变化率)为某一定值时绝缘线对ef的拉力恰好为零.在这种情况下: