题目内容
【题目】在用两面平行的玻璃砖测定玻璃折射率的实验中，其实验光路如图，
（1）在实验中，如果用量角器分别量出入射角θ1和折射角θ2，那么，该玻璃砖的折射率的表达式为n=____
（2）在实验数据的处理中，有两位同学各设计了一个记录表格，而且都已完成了计算，根据他们设计的表格所反应的信息，判断他们论证做得是否正确.
甲同学设计的表格是：
次数 | 入射角θ1 | sinθ1 | 折射角θ2 | sinθ2 | n |
|
1 | 30° | 0.500 | 20.9° | 0.357 | 1.40 | 1.40 |
2 | 45° | 0.707 | 30.5° | 0.508 | 1.39 | |
3 | 60° | 0.866 | 38.0° | 0.616 | 1.41 |
乙同学设计的表格是：
次数 | 1 | 2 | 3 | 角平均值 | 正弦值 | n |
入射角θ1 | 30° | 45° | 60° | 45° | 0.707 | 1.42 |
折射角θ2 | 20.9° | 30.5° | 38.0° | 28.8° | 0.497 |
答：上述两位同学做得正确的是____.（填“甲”或“乙”）
（3）若甲在做测定玻璃的折射率的实验时，法线画得与界面不垂直,出现如下图（a）所示的倾斜；若乙在放置玻璃砖时,玻璃砖的平面没有与aa′重合，出现如下图（b）所示的偏差，则他们测得的折射率比真实值____
A. 甲、乙均偏小
B. 甲、乙均偏大
C. 甲偏大、乙偏小
D. 甲偏小，乙偏大
【答案】 （1）
（2）甲 （3）A
【解析】（1）根据光的折射定律可知： 
；
（2）为了减小测量的偶然误差，必须采用多次测量取平均值的方法．由于每次测量时，入射角不同，折射角不同，每次测量有入射角与折射角之间没有直接关系，入射角和折射角取平均值没有意义．而介质的折射率仅由介质的性质决定，是不变的，所以应求出每一个入射角及对应的折射角，运用折射定律求出折射率，再求出折射率的平均值，可有效减小测量的误差，这样做有意义．故甲同学做得正确．
（3）（a）测得的入射角i和折射角r都偏大，而且增大相同的角度．玻璃砖的折射率为： 
，运用特殊值法分析：
假设若法线与界面垂直时，入射角为i=45°，折射角为r=30°，则折射率为： 
若法线与界面不垂直时，入射角与折射角都增大15°，则折射率为：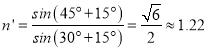 
，可见，甲的测量值将偏小．
（b）出现如图（b）所示的偏差时测量的入射角i和折射角r都增大，而且增大相同的角度．与a情况恰好相同，故测量值将偏小，故A正确，BCD错误；故选A．
