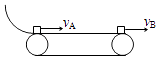题目内容
【题目】一辆汽车正以15m/s的速度在平直公路上前进，突然发现正前方有一辆自行车以5m/s的速度做同方向的匀速直线运动，汽车立即关闭油门做加速度大小为5m/s2的匀减速运动，汽车恰好不碰上自行车，求关闭油门时汽车离自行车的距离．
【答案】解：设汽车关闭发动机后离自行车的距离为x0，汽车经过t时间恰好不碰到自行车，则：
位移关系有：x汽=x0+x自
由运动学公式有：
x汽=v0t+ 
at2
x自=v自t
速度关系有：v自=v0﹣at
得：x0=10m
答：关闭油门时汽车离自行车的距离是10m．
【解析】追击相遇问题要注意一个条件，两个关系。一个条件是指两物体速度相等时是距离最大最远的条件。两个关系是指时间关系和位移关系。汽车恰好不碰到自行车的临界条件。是两物体速度相等。
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系的相关知识点，需要掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值才能正确解答此题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
