题目内容
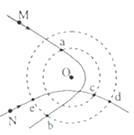
【题目】如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L。在△OCA区域内有垂直于xOy平面向里的匀强磁场。质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场。已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0。不计重力。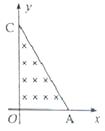
①求磁场的磁感应强度的大小;
②若粒子先后从两不同点以相同的速度射入磁场,恰好从OC边上的同一点射出磁场,求该粒子这两次在磁场中运动的时间之和;
③若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为 ![]() ,求粒子此次入射速度的大小。
,求粒子此次入射速度的大小。
【答案】解:①粒子在磁场中做匀速圆周运动,在时间 ![]() 内其速度方向改变了
内其速度方向改变了 ![]() ,故其周期:
,故其周期: ![]() ①设磁感应强度大小为B,粒子速度为 v ,圆周运动的半径为 r ,由洛伦兹力公式和牛顿定律得:
①设磁感应强度大小为B,粒子速度为 v ,圆周运动的半径为 r ,由洛伦兹力公式和牛顿定律得:![]() ②
②
匀速圆周运动的速度满足: ![]() ③
③
联立①②③式得: ![]() ④
④
②设粒子从OA变两个不同位置射入磁场,能从OC边上的同一点P射出磁场,粒子在磁场中运动的轨迹如图(a)所示: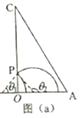
设两轨迹所对应的圆心角分别为 ![]() 和
和 ![]() 。由几何关系有:
。由几何关系有: ![]() ⑤粒子两次在磁场中运动的时间分别为 t1 与 t2 ,则:
⑤粒子两次在磁场中运动的时间分别为 t1 与 t2 ,则: ![]() ⑥③如图(b),由题给条件可知,该粒子在磁场区域中的轨迹圆弧对应的圆心角为
⑥③如图(b),由题给条件可知,该粒子在磁场区域中的轨迹圆弧对应的圆心角为 ![]() 。设
。设 ![]() 为圆弧的圆心,圆弧的半径为 r0 ,圆弧与AC相切与B点,从D点射出磁场,由几何关系和题给条件可知,此时有
为圆弧的圆心,圆弧的半径为 r0 ,圆弧与AC相切与B点,从D点射出磁场,由几何关系和题给条件可知,此时有![]() ⑦
⑦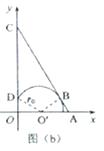
![]() ⑧
⑧
设粒子此次入射速度的大小为 v0 ,由圆周运动规律: ![]() ⑨
⑨
联立①⑦⑧⑨式得:![]() ⑩
⑩
【解析】(1)粒子垂直OA进入磁场中,转过90°,垂直打在y轴上,则 ![]() ,求出周期,由周期公式T=
,求出周期,由周期公式T= ![]() 求B的大小.(2)画出两个粒子的运动轨迹,设轨迹所对应的圆心角分别为θ1和θ2 , 由几何关系有θ1=180°-θ2 , 可得到时间之和等于
求B的大小.(2)画出两个粒子的运动轨迹,设轨迹所对应的圆心角分别为θ1和θ2 , 由几何关系有θ1=180°-θ2 , 可得到时间之和等于 ![]() .(3)根据圆周运动知识知道,两粒子在磁场中运动的时间差△t与△θ=θ2-θ1成正比,只要求出△θ的最大值,即可求得θ2的最大值.由△t=
.(3)根据圆周运动知识知道,两粒子在磁场中运动的时间差△t与△θ=θ2-θ1成正比,只要求出△θ的最大值,即可求得θ2的最大值.由△t= ![]() T和已知条件△tmax=
T和已知条件△tmax= ![]() ,联立可求出θ2的最大值,再结合几何知识求出轨迹的半径,由牛顿第二定律,利用洛伦兹力等于向心力,列式求解速度.
,联立可求出θ2的最大值,再结合几何知识求出轨迹的半径,由牛顿第二定律,利用洛伦兹力等于向心力,列式求解速度.

【题目】小明同学通过实验探究某一金属电阻的阻值R随温度t的变化关系.已知该金属电阻在常温下的阻值约10 Ω,R随t的升高而增大.实验电路如图所示,控温箱用以调节金属电阻的温值.实验时闭合S,先将开关K与1端闭合,调节金属电阻的温度,分别记下温度t1 , t2 , …和电流表的相应示数I1 , I2 , ….然后将开关K与2端闭合,调节电阻箱使电流表的实数再次为I1 , I2 , …,分别记下电阻箱相应的示数R1 , R2 , ….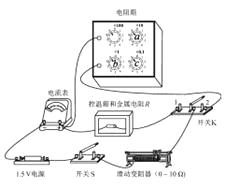
(1)有以下两电流表,实验电路中应选用______.
A.量程0~100 mA,内阻约2Ω
B.量程0~0.6 A,内阻可忽略
(2)实验过程中,要将电阻箱的的阻值由9.9 Ω调节至10.0Ω,需旋转图中电阻箱的旋钮“a”、“b”、“c”,正确的操作顺序是.
①将旋钮a由“0”旋转至“1”
②将旋钮b由“9”旋转至“0”
③将旋钮c 由“9”旋转至“0”
(3)实验记录的t和R的数据见下表:
温度t(℃) | 20.0 | 40.0 | 60.0 | 80.0 | 100.0 |
阻值R(Ω) | 9.6 | 10.4 | 11.1 | 12.1 | 12.0 |
请根据表中数据,在答题卡的方格纸上作出R—t图象.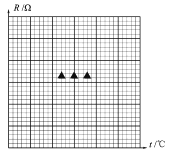
由图线求得R随t的变化关系为R=。