题目内容
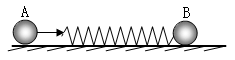
如图所示，在光滑的水平面上静止放一质量为m的木 板B，木板表面光滑，左端固定一轻质弹簧。质量为2m的木块A以速度v0从板的右端水平向左滑上木板B。在木块A与弹簧相互作用的过程中，下列判断正确的是
A.弹簧压缩量最大时，B板运动速率最大
B.B板的加速度一直增大
C.弹簧给木块A的冲量大小为2mv0/3
D.弹簧的最大弹性势能为mv02/3
D
解析试题分析：当A向左压缩弹簧时A物块减速，B板做加速度增大的加速运动，当弹簧压缩量最大时，A、B共速，之后弹簧在恢复形变的过程中B板做加速度减小的加速，A物块继续减速，当弹簧恢复原长时B板达最大速度，所以AB选项均错；当弹簧恢复原长时，设A、B的速度分别为
和
，由动量守恒定律，
，能量守恒定律有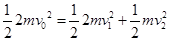
，联立解得：
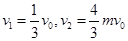，弹簧给木块A的冲量I=2mv1-2mv0=-4mv0/3，所以弹簧给木块A的冲量大小为4mv0/3，C选项错误；弹簧最大的弹性势能发生在AB共速时，设共速的速度为
，由动量守恒知
，
再由
，所以D选项正确。
考点：动量守恒定律 能量守恒定律
名师点拨卷系列答案
英才计划期末调研系列答案 木块a和b用一根轻弹簧连接起来，放在光滑水平面上，a紧靠在墙壁上．在b上施加向左的水平力F使弹簧压缩，如图所示．当撤去外力F后，下列说法中正确的是（ ）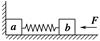
| A．a尚未离开墙壁前，a和b组成的系统动量守恒 |
| B．a尚未离开墙壁前，a和b组成的系统动量不守恒 |
| C．a离开墙壁后，a、b组成的系统动量守恒 |
| D．a离开墙壁后，a、b组成的系统动量不守恒 |
质量为M、内壁间距为L的箱子静止于光滑的水平面上，箱子中间有一质量为m的小物块，小物块与箱子底板间的动摩擦因数为μ。初始时小物块停在箱子正中间，如图所示。现给小物块一水平向右的初速度v，小物块与箱壁碰撞N次后恰又回到箱子正中间，井与箱子保持相对静止。设碰撞都是弹性的，则整个过程中，系统损失的动能为 
A． | B． | C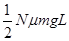． | D．(N-1)μmgL |
（５分）如图所示,将质量为M1,半径为R且内壁光滑的半圆槽置于光滑水平面上,左侧靠墙角,右侧靠一质量为M2的物块.今让一质量为m的小球自左侧槽口A的正上方h高处从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是（ ）
| A．小球在槽内运动的全过程中,小球与半圆槽在水平方向动量守恒 |
| B．小球在槽内运动的全过程中,小球、半圆槽和物块组成的系统动量守恒 |
| C．小球离开C点以后,将做竖直上抛运动 |
| D．槽将与墙不会再次接触 |
质量相等的三个物体在一光滑水平面上排成一直线，且彼此隔开一定距离，如图，具有初动能E0的第一号物块向右运动，依次与其余两个物块发生碰撞，最后这三个物体粘成一个整体，这个整体的动能等于
| A．E0 | B． 2E0/3 | C． E0/3 | D． E0/9 |
质量都为m的小球a、b、c以相同的速度分别与另外三个质量都为M的静止小球相碰后，a球被反向弹回，b球与被碰球粘合在一起仍沿原方向运动，c球碰后静止，则下列说法正确的是( )
| A．m一定大于M |
| B．m可能等于M |
| C．b球与质量为M的球组成的系统损失的动能最大 |
| D．c球与质量为M的球组成的系统损失的动能最大 |
，试求：