题目内容
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ。初始时小物块停在箱子正中间,如图所示。现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,井与箱子保持相对静止。设碰撞都是弹性的,则整个过程中,系统损失的动能为 
A. | B. | C.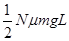 | D.(N-1)μmgL |
B
解析试题分析:物块与箱子所组成的系统动量守恒,满足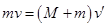 ,所以可知整个过程中系统损失的动能
,所以可知整个过程中系统损失的动能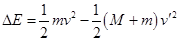 ,联立解得
,联立解得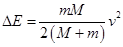 ,故只有选项B正确;
,故只有选项B正确;
考点:动量守恒定律

练习册系列答案
相关题目
如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,木板质量M=3kg。质量m=1kg的铁块以水平速度v0=4m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端。在上述过程中弹簧具有的最大弹性势能为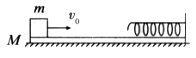
| A.3J | B.4J | C.6J | D.20J |
(6分)一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1∶16,有:( )
| A.该原子核发生了α衰变 |
| B.该原子核发生了β衰变 |
| C.那个打出衰变粒子的反冲核沿小圆作逆时针方向运动 |
| D.该衰变过程结束后其系统的总质量略有增加 |
 =4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为
=4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为

