题目内容
【题目】如下图1所示，abcd是位于竖直平面内的正方形闭合金属线框，其质量为0.04kg，电阻为0.4Ω。在金属线框的下方有一匀强磁场区域，MN和PQ是该匀强磁场区域的水平边界，并与线框的bc边平行，磁场方向与线框平面垂直，磁场区域上下边界的距离大于线框的边长。现金属线框由距MN某一高度处从静止开始下落，经时间0.1s后刚好到达MN边缘，速度为0.8m/s，线框所受空气阻力恒定。下图2是金属线框由静止开始下落到ad边刚好进入磁场区域运动过程的v-t图像，g=10m/s2。
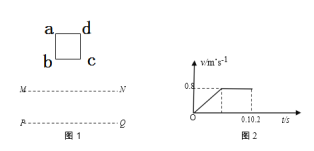
（1）bc边从刚好进入磁场区域到将要离开这一区域的过程中线框做的是怎样的运动？线框的边长是多少m?
（2）bc边刚好离开磁场区域时线框的加速度方向是怎样的？
（3）求线框从开始运动到ad边刚好进入磁场的运动过程中空气阻力做的功；
（4）求磁场的磁感应强度。
【答案】（1）先匀速直线运动，后匀加速直线运动，0.08m（2）竖直向上（3）-0.0096J（4）5T
【解析】
（1）由图2可知，bc边从刚好进入磁场区域时做匀变速直线运动，当线框全部进入磁场中，线框中没感应电流，只受到重力和阻力的作用，开始做匀速加速直线运动，直到bc边到达磁场边界PQ，即线框先匀速直线运动，后匀加速直线运动。
线框的边长为：
。
（2）线框匀速进入磁场，线框进入磁场方程线框受到的安培力和阻力的合力等于重力，线框完全进入磁场后做匀加速运动，线框bc边刚离开磁场时的速度大于线框进入磁场时的速度，此时线框受到的安培力和阻力的合力大于重力，线框受到的合力向上，线框的加速度向上。
（3）线框进入磁场前的加速度为
由牛顿第二定律可得：
由以上方程解得：
线框加速下落的高度为：
所以线框从开始运动到ad边刚好进入磁场的运动方程中空气阻力做的功：
（4）线框进入磁场过程中做匀速运动，由平衡条件可得：
代入数据可得安培力大小：
线框受到的安培力为：
代入数据可得：
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
