题目内容
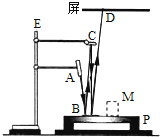
【题目】为了探究加速度与力、质量的关系,甲、乙、丙三位同学分别设计了如图所示的实验装置,小车总质量用M表示(乙图中M包括小车与传感器,丙图中M包括小车和与小车固连的滑轮),钩码总质量用m表示.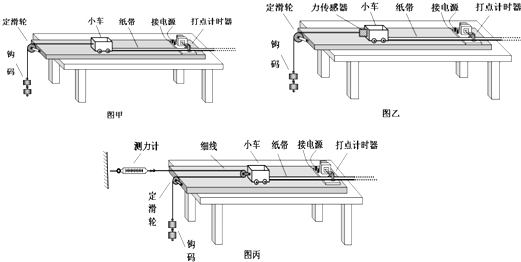
(1)图丁是用图甲装置中打点计时器所打的纸带的一部分,O,A,B,C,D和E为纸带上六个计数点,加速度大小用a表示.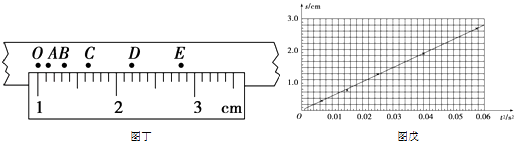
则OD间的距离为 cm.图戊是根据实验数据绘出的s﹣t2图线(s为各计数点至同一起点的距离),则加速度大小a=m/s2(保留三位有效数字)
(2)若乙、丙两位同学发现某次测量中力传感器和测力计读数相同,通过计算得到小车加速度均为a,g为当地重力加速度,则乙、丙两人实验时所用小车总质量之比为 .
【答案】
(1)1.20;0.933
(2)1:2
【解析】解:(1)由图示刻度尺可知,OD间的距离为:2.20cm﹣1.00cm=1.20cm;
小车做初速度为零的匀加速直线运动,则:s= ![]() at2 , 由图示图象可知:k=
at2 , 由图示图象可知:k= ![]() a,则a=2k=2×
a,则a=2k=2× ![]() ≈0.933m/s2;(2)乙、丙两位同学发现某次测量中力传感器和测力计读数相同,且通过计算得到小车加速度均为a,
≈0.933m/s2;(2)乙、丙两位同学发现某次测量中力传感器和测力计读数相同,且通过计算得到小车加速度均为a,
根据牛顿第二定律,则有:F=M乙a,2F=M丙a;
因此乙、丙两人实验时所用小车总质量之比为1:2;
由牛顿第二定律,对砝码研究,则有m乙g﹣F=m乙a,
而m丙g﹣F=m丙2a,
解得,m乙:m丙=1:2;
所以答案是:(1)1.20,0.933;(2)1:2.

练习册系列答案
相关题目