题目内容
20.我国将要发射一颗绕月运行的探月卫星“嫦娥1号”.设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量为地球质量的$\frac{1}{80}$,月球的半径约为地球半径的$\frac{1}{4}$,地球上的第一宇宙速度约为7.9km/s,则该探月卫星绕月运行的速率约为( )| A. | 0.4 km/s | B. | 1.8 km/s | C. | 11 km/s | D. | 36 km/s |
分析 根据万有引力提供向心力得出第一宇宙速度的表达式,从而得出线速度的关系,求出探月卫星绕月运行的速率.
解答 解:根据$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$得,v=$\sqrt{\frac{GM}{R}}$,因为月球的质量为地球的质量$\frac{1}{80}$,月球的半径约为地球半径的$\frac{1}{4}$,则速度之比为$\sqrt{\frac{1}{20}}$,
所以探月卫星绕月运行的速率$v′=7.9×\sqrt{\frac{1}{20}}km/s$=1.8km/s.
故选:B.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道第一宇宙速度的轨道半径等于中心天体的半径.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
8.如图,光滑水平面上,质量为m的子弹以v的速度水平射入木块(木块质量为M )后留在木块内,则( )


| A. | 木块的最大速度为$\frac{mv}{M+m}$ | |
| B. | 子弹射入木块的过程中,子弹受到的冲量为$\frac{mMv}{M+m}$ | |
| C. | 若将子弹、木块和弹簧合在一起作为研究对象(系统),此系统从子弹开始射入到弹簧压缩到最短的整个过程中,动量守恒 | |
| D. | 弹簧的最大弹性势能为$\frac{m{v}^{2}}{2}$ |
5.如图,汽车以速度V通过一半圆形拱桥的顶点时,关于汽车受力的说法正确的是( )


| A. | 汽车受重力、支持力、向心力 | |
| B. | 汽车受重力、支持力、牵引力、摩擦力、向心力 | |
| C. | 重力提供汽车的向心力 | |
| D. | 汽车的重力和支持力的合力提供向心力 |
9. 如图,滑块A和B叠放在固定的斜面体上,从静止开始以相同的加速度一起沿斜面加速下滑.已知B与斜面体间光滑接触,则在AB下滑的过程中,下列说法正确的是( )
如图,滑块A和B叠放在固定的斜面体上,从静止开始以相同的加速度一起沿斜面加速下滑.已知B与斜面体间光滑接触,则在AB下滑的过程中,下列说法正确的是( )
 如图,滑块A和B叠放在固定的斜面体上,从静止开始以相同的加速度一起沿斜面加速下滑.已知B与斜面体间光滑接触,则在AB下滑的过程中,下列说法正确的是( )
如图,滑块A和B叠放在固定的斜面体上,从静止开始以相同的加速度一起沿斜面加速下滑.已知B与斜面体间光滑接触,则在AB下滑的过程中,下列说法正确的是( )| A. | B对A的支持力不做功 | B. | B对A的摩擦力做负功 | ||
| C. | B对A的合力不做功 | D. | B对A的合力做正功 |

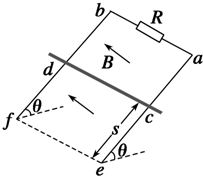 如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ.
如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ. 如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=2.5m,轨道在C处与水平地面相切.在C处放质量为m=1kg的一小物块,给它一水平向左的初速度v0=10$\sqrt{2}$m/s,结果它沿CBA运动,并能通过A点,最后落在水平面上的D点,求:
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=2.5m,轨道在C处与水平地面相切.在C处放质量为m=1kg的一小物块,给它一水平向左的初速度v0=10$\sqrt{2}$m/s,结果它沿CBA运动,并能通过A点,最后落在水平面上的D点,求: 如图所示,一辆质量为500kg的汽车静止在一座半径为40m的圆弧形拱桥顶部(g=10m/s2),求:
如图所示,一辆质量为500kg的汽车静止在一座半径为40m的圆弧形拱桥顶部(g=10m/s2),求: