题目内容
7.如图1所示,匀强磁场的磁感应强度B为0.5T,其方向垂直于倾角θ=30°的斜面向上.绝缘斜面上固定有“V”字形的光滑金属导轨MON(电阻忽略不计),MO和NO长度均为S=2.5m,MN连线水平,MN两点间距离为D=3m,P为MN的中点,以O为原点,OP为x轴建立一维坐标系Ox,一根粗细均匀的金属杆CD,长度d=3.0m,质量m=1kg,电阻R=0.3Ω,在拉力F的作用下,从O处以恒定速度v=1m/s在导轨上沿x轴正向运动(金属杆与导轨接触良好),g取10m/s2.(1)求金属杆CD运动到x=0.8m处时,金属杆中电流强度的大小和方向;
(2)推导金属杆CD从O处运动到MN处过程中拉力F与位置坐标x的关系式,并在图2中画出F-x关系图象;
(3)求金属杆CD从O点运动到MN处的全过程中产生的焦耳热.

分析 (1)导体棒切割磁感线产生感应电动势,由几何关系求得x=0.8m处的电动势,由欧姆定律求出感应电流,由右手定则判断出电流方向;
(2)应用E=BLv求出感应电动势,由欧姆定律求出电流,由安培力公式求出安培力,然后由平衡条件求出拉力F,最后作出图象;
(3)当导体棒匀速运动,由有效长度可列出安培力大小关于向上运动位移的表达式,根据安培力与位移成线性关系,可利用安培力平均值来求出产生焦耳热.
解答 解:(1)设∠PON=α,由题意可知:sinα=$\frac{PN}{ON}$=$\frac{\frac{3}{2}}{2.5}$=$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=0.75,
金属杆CD运动到x=0.8m处时切割磁感线的有效长度:L=2xtanα=1.2m,
此时产生的感应电动势:E=BLv=0.5×1.2×1=0.6V,
接入电路的电阻:r=$\frac{L}{d}$R=$\frac{1.2}{3}$×0.3=0.12Ω,
电路电流:I=$\frac{E}{r}$=$\frac{0.6}{0.12}$=5A,
由右手定则可知,感应电流方向为:由C流向D;
(2)金属棒切割磁感线的有效长度:L=2xtanα=1.5x,
金属棒接入电路的电阻阻值:r=$\frac{L}{d}$R=0.15xΩ,
感应电动势:E=BLv,
感应电流:I=$\frac{E}{r}$=$\frac{BLv}{r}$=$\frac{0.5×1.5x×1}{0.15x}$=5A,
金属棒受到的安培力:F安=BIL=0.5×5×1.5x=3.75x,
金属棒做匀速直线运动,由平衡条件得:mgsinθ+F安=F,
解得:F=5+3.75x,x=0时,F=5N,x=2m时,F=12.5N,F-x关系图象如图:
(3)设导体棒经t时间沿导轨匀速向上运动的位移为x,
金属棒的最大位移:x=ONcosα=2m,
导体棒在导轨上运动时所受的安培力:F安=3.75x,
因安培力的大小F安与位移x成线性关系,故通过导轨过程中导体棒所受安培力的平均值:
$\overline{F}$=$\frac{0+3.75×2}{2}$=3.75N,
产生的焦耳热:Q=$\overline{F}$x=3.75×2=7.5J;
答:(1)金属杆CD运动到x=0.8m处时,金属杆中电流强度的大小为5A,方向:由C流向D;
(2)金属杆CD从O处运动到MN处过程中拉力F与位置坐标x的关系式为:F=5+3.75x,F-x关系图象如图所示;
(3)金属杆CD从O点运动到MN处的全过程中产生的焦耳热为7.5J.
点评 考查法拉第电磁感应定律,闭合电路欧姆定律,共点力平衡条件及安培力表达式.本题突破口:产生感应电流与导体棒有效长度无关,同时巧用安培力与位移成线性关系,由安培力平均值来求焦耳热.

 阅读快车系列答案
阅读快车系列答案 如图,两个斜面的倾角分别为45°和60°.物块m分别从两个斜面顶端沿斜面做两次滑动,已知物块与两个斜面间的动摩擦因数均为μ,则物块从斜面顶端滑至底端的过程中克服摩擦力做的功为( )
如图,两个斜面的倾角分别为45°和60°.物块m分别从两个斜面顶端沿斜面做两次滑动,已知物块与两个斜面间的动摩擦因数均为μ,则物块从斜面顶端滑至底端的过程中克服摩擦力做的功为( )| A. | 沿45°角的斜面滑下较大 | B. | 沿60°角的斜面滑下较大 | ||
| C. | 一样大 | D. | 无法确定 |
| A. | 木箱沿光滑斜面下滑的过程 | |
| B. | 电梯加速上升的过程 | |
| C. | 雨滴在空中匀速下落的过程 | |
| D. | 游客在摩天轮中随摩天轮在竖直面内匀速转动的过程 |
| A. | 0.4 km/s | B. | 1.8 km/s | C. | 11 km/s | D. | 36 km/s |
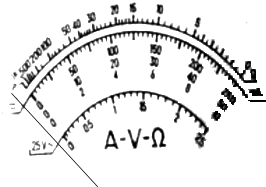 某同学为了测定一个电阻的阻值,进行了如下的操作:
某同学为了测定一个电阻的阻值,进行了如下的操作: 如图所示,在内壁光滑的平底试管内放一个小球,试管的开口端与水平轴O连接,让试管在竖直平面内匀速转动.已知转动轴到管底小球的距离L=5cm,在试管转动过程中,小球做匀速圆周运动,试管底部对小球弹力的最大值是最小值的3倍.求:试管转动的角速度ω(g取10m/s2).
如图所示,在内壁光滑的平底试管内放一个小球,试管的开口端与水平轴O连接,让试管在竖直平面内匀速转动.已知转动轴到管底小球的距离L=5cm,在试管转动过程中,小球做匀速圆周运动,试管底部对小球弹力的最大值是最小值的3倍.求:试管转动的角速度ω(g取10m/s2).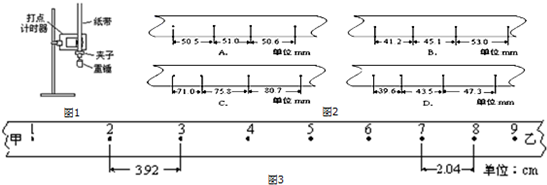
 如图一横截面为扇形的玻璃砖,半径为R,∠ABC=135°,一束平行光照射到BC面上,方向与BA平行,玻璃对光的折射率为$\sqrt{2}$,求光能从圆弧面上射出部分的弦长.
如图一横截面为扇形的玻璃砖,半径为R,∠ABC=135°,一束平行光照射到BC面上,方向与BA平行,玻璃对光的折射率为$\sqrt{2}$,求光能从圆弧面上射出部分的弦长.