题目内容
11.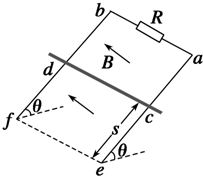 如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ.
如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ.求:(1)金属棒上滑过程中的最大速度;
(2)金属棒下滑过程的末速度;
(3)金属棒自ef端上滑再回到ef端的过程中,电阻R产生的焦耳热.
分析 (1)当棒的加速度为零时,棒的速度最大.根据共点力平衡求出EF下滑的最大速度.
(2)金属棒下滑到ef时已经做匀速运动,用与上题同样的方法求金属棒下滑过程的末速度.
(3)棒先向上减速至零,然后从静止加速下滑,在滑回ef之前已达最大速度开始匀速,结合能量守恒定律求出电阻R上产生的焦耳热.
解答 解:(1)金属棒上滑过程中,加速度为零时速度最大,设最大速度为v1,此时棒所受的安培力:F安=BIL=B•$\frac{BL{v}_{1}}{R}$L=$\frac{{B}^{2}{L}^{2}{v}_{1}}{R}$
根据平衡条件得:mgsinθ+F安+μmgcosθ=F
解得:v1=$\frac{(F-mgsinθ-μmgcosθ)R}{{B}^{2}{L}^{2}}$
(2)设金属棒下滑过程的末速度为v2,此时棒做匀速运动,则有:
mgsinθ=μmgcosθ+$\frac{{B}^{2}{L}^{2}{v}_{2}}{R}$
解得:v2=$\frac{mg(sinθ-μcosθ)R}{{B}^{2}{L}^{2}}$.
(3)金属棒自ef端上滑再回到ef端的过程中,设电阻R产生的焦耳热为Q.
根据能的转化与守恒定律:
Q=Fs-2μmgscosθ-$\frac{1}{2}m{v}_{2}^{2}$=Fs-2μmgscosθ-$\frac{m{g}^{2}(sinθ-μcosθ)^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$
答:
(1)金属棒上滑过程中的最大速度是$\frac{(F-mgsinθ-μmgcosθ)R}{{B}^{2}{L}^{2}}$;
(2)金属棒下滑过程的末速度是$\frac{mg(sinθ-μcosθ)R}{{B}^{2}{L}^{2}}$;
(3)金属棒自ef端上滑再回到ef端的过程中,电阻R产生的焦耳热是Fs-2μmgscosθ-$\frac{m{g}^{2}(sinθ-μcosθ)^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$.
点评 本题综合考查了共点力平衡、能量守恒定律,综合性较强,关键要能推导出安培力与速度的关系式,正确分析能量是如何转化的.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案| A. | 木箱沿光滑斜面下滑的过程 | |
| B. | 电梯加速上升的过程 | |
| C. | 雨滴在空中匀速下落的过程 | |
| D. | 游客在摩天轮中随摩天轮在竖直面内匀速转动的过程 |
| A. | 物体滑至底端时的速度相同 | B. | 到达底端时重力的即时功率相同 | ||
| C. | 物体受到的重力冲量相同 | D. | 物体下滑时合外力做的功相同 |
| A. | 0.4 km/s | B. | 1.8 km/s | C. | 11 km/s | D. | 36 km/s |
 某同学为了测定一个电阻的阻值,进行了如下的操作:
某同学为了测定一个电阻的阻值,进行了如下的操作: 如图一横截面为扇形的玻璃砖,半径为R,∠ABC=135°,一束平行光照射到BC面上,方向与BA平行,玻璃对光的折射率为$\sqrt{2}$,求光能从圆弧面上射出部分的弦长.
如图一横截面为扇形的玻璃砖,半径为R,∠ABC=135°,一束平行光照射到BC面上,方向与BA平行,玻璃对光的折射率为$\sqrt{2}$,求光能从圆弧面上射出部分的弦长.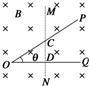 如图所示,有一弯成θ=37°角的光滑金属导轨POQ,水平放置在磁感应强度为B=2T的匀强磁场中,磁场方向与导轨平面垂直.有一金属棒MN与导轨的OQ边垂直放置,金属棒从离O点右侧L0=10cm处静止开始以加速度a=0.2m/s2向右运动,求t=2秒末时,棒与导轨所构成的回路中的感应电动势多少?如果导体单位长度电阻为R0=2Ω,则导体中电流是多少?
如图所示,有一弯成θ=37°角的光滑金属导轨POQ,水平放置在磁感应强度为B=2T的匀强磁场中,磁场方向与导轨平面垂直.有一金属棒MN与导轨的OQ边垂直放置,金属棒从离O点右侧L0=10cm处静止开始以加速度a=0.2m/s2向右运动,求t=2秒末时,棒与导轨所构成的回路中的感应电动势多少?如果导体单位长度电阻为R0=2Ω,则导体中电流是多少?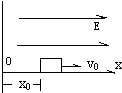 一个质量为m、带有电荷-q的小物体距O点为x0,可在水平轨道Ox上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿Ox正方向,如图所示,小物体以初速度v0沿Ox轴正方向运动,运动时受到大小不变的摩擦力f的作用,且f<qE,设小物体与墙碰撞时不损失机械能,且电荷量保持不变,求它停止运动前所通过的路程?
一个质量为m、带有电荷-q的小物体距O点为x0,可在水平轨道Ox上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿Ox正方向,如图所示,小物体以初速度v0沿Ox轴正方向运动,运动时受到大小不变的摩擦力f的作用,且f<qE,设小物体与墙碰撞时不损失机械能,且电荷量保持不变,求它停止运动前所通过的路程? “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.