题目内容
17.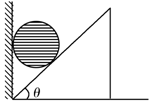 如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )| A. | 斜劈对小球的弹力不做功 | |
| B. | 小球的重力势能减小动能增加,所以小球的机械能守恒 | |
| C. | 小球机械能的减小量等于斜劈动能的增加量 | |
| D. | 斜劈与小球组成的系统机械能守恒 |
分析 小球和斜劈组成的系统中,只有重力势能和动能相互转化,机械能守恒;而小球和斜劈的机械能都不守恒.
解答 解:A、斜劈由静到动,动能增加,只有弹力对斜劈做功,根据动能定理,斜劈对小球的弹力做负功,小球的机械能不守恒,故AB错误;
C、小球和斜劈组成的系统中,只有重力势能和动能相互转化,机械能守恒,故球机械能的减小量等于斜劈动能的增加量,故CD正确
故选:CD
点评 本题关键分析清楚物体的运动和能量的转化情况,要明确是小球和斜劈组成的系统机械能守恒,而不是单个物体机械能守恒.

练习册系列答案
相关题目
18. 如图所示,质量为58g的网球,以v1=40m/s的速度水平飞来,运动员以60m/s的速度反拍击回的过程中,网球的动量变化为( )
如图所示,质量为58g的网球,以v1=40m/s的速度水平飞来,运动员以60m/s的速度反拍击回的过程中,网球的动量变化为( )
 如图所示,质量为58g的网球,以v1=40m/s的速度水平飞来,运动员以60m/s的速度反拍击回的过程中,网球的动量变化为( )
如图所示,质量为58g的网球,以v1=40m/s的速度水平飞来,运动员以60m/s的速度反拍击回的过程中,网球的动量变化为( )| A. | 大小为1.16kg•m/s,方向v1方向相同 | |
| B. | 大小为1.16kg•m/s,方向v1方向相反 | |
| C. | 大小为5.8kg•m/s,方向v1方向相同 | |
| D. | 大小为5.8kg•m/s,方向v1方向相反 |
8.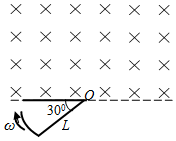 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
 如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )
如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B.电阻为R、半径为L、圆心角为30°的扇形闭合导线框绕垂直于纸面的o轴以角速度ω匀速转动(o轴位于磁场边界).则线框内产生的感应电流的有效值为( )| A. | $\frac{B{L}^{2}ω}{72R}$ | B. | $\frac{\sqrt{6}B{L}^{2}ω}{12R}$ | C. | $\frac{\sqrt{2}B{L}^{2}ω}{4R}$ | D. | $\frac{\sqrt{3}B{L}^{2}ω}{2R}$ |
5.若宇航员在某行星和地球上相对于各自的水平地面附近相同的高度,将一个物体由静止释放,它们落地时间之比为2:1,已知该行星质量是地球质量的9倍,地球表面重力加速度为g,地球半径为R,下列分析正确的是( )
| A. | 该行星表面的重力加速度为$\frac{1}{2}$g | B. | 该行星表面的重力加速度为$\frac{1}{4}$g | ||
| C. | 该行星的半径为6R | D. | 该行星的密度比地球的密度大 |
2.某人用绳提着质量为m的物体,使物体以加速度a(a<g)沿竖直方向加速下降高度h;稍停后,此人再用绳提着该物体以加速度a沿竖直方向加速提升高度h.这两个过程中人对物体做的总功为( )
| A. | 2mah | B. | 0 | C. | 2mgh | D. | m(g+a)h |
7. 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )| A. | m能到达圆弧轨道右侧的最高位置与初始位置等高 | |
| B. | m能到达圆弧轨道右侧的最高位置比初始位置低,不会滑出圆弧轨道 | |
| C. | m能到达圆弧轨道右侧的最高位置比初始位置高,将滑出圆弧轨道 | |
| D. | m到达圆弧轨道右侧最高位置时,M将会向左移动一段位移 |
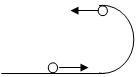 如图所示,质量为1kg小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R=0.4m,小球从最高点离开轨道落到地面时速度方向与水平面夹角为53°.(sin53°=0.8 cos53°=0.6)求:(g=10m/s2)
如图所示,质量为1kg小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R=0.4m,小球从最高点离开轨道落到地面时速度方向与水平面夹角为53°.(sin53°=0.8 cos53°=0.6)求:(g=10m/s2) 如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求:
如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求: