题目内容
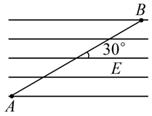
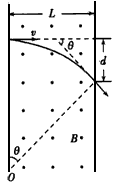
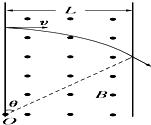 带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度 v=3.2×106m/s 沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.求:
带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度 v=3.2×106m/s 沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.求:(1)带电粒子离开磁场时的偏转角多大?
(2)带电粒子在磁场中运动多长时间?
分析:(1)带电粒子在匀强磁场中做匀速圆周运动,由提供的数据可解半径数值,结合磁场宽度可解圆心角度数,由几何关系可得偏转角;
(2)由洛伦兹力提供向心力求得周期公式,由运动径迹得到圆弧运动时间与周期的关系,进而求出时间.
(2)由洛伦兹力提供向心力求得周期公式,由运动径迹得到圆弧运动时间与周期的关系,进而求出时间.
解答:解:(1)带电粒子在磁场中做匀速圆周运动,速度大小不变,故离开磁场时为:
v=3.2×106 m/s,
由题意得:R=
=
m=0.2m.
由几何关系得:sinθ=
=
,即速度偏转角度θ=30°.
(2)粒子在磁场中运动的时间:t=
T,且T=
,
可得:t=
=
s=3.3×10-8 s,
答:(1)粒子离开磁场时的速度偏转30°;
(2)粒子在磁场中运动的时间是3.3×10-8s.
v=3.2×106 m/s,
由题意得:R=
| mv |
| qB |
| 1.7×10-27×3.2×106 |
| 1.6×10-19×0.17 |
由几何关系得:sinθ=
| L |
| R |
| 1 |
| 2 |
(2)粒子在磁场中运动的时间:t=
| θ |
| 360° |
| 2πm |
| qB |
可得:t=
| πm |
| 6qB |
| 3.14×1.7×10-27 |
| 6×1.6×10-19×0.17 |
答:(1)粒子离开磁场时的速度偏转30°;
(2)粒子在磁场中运动的时间是3.3×10-8s.
点评:本题考查带电粒子在磁场中的运动,重点是画出轨迹,分析轨迹中的几何关系,结合带带电粒子的半径和周期公式求解.

练习册系列答案
相关题目
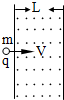 带电粒子的质量m=1.7×10-27Kg,电量q=1.6×10--19C,以速度v=3.2×10-6m/s沿垂直于磁场同时又垂直于磁场边界的方向射入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.不计粒子重力.求:
带电粒子的质量m=1.7×10-27Kg,电量q=1.6×10--19C,以速度v=3.2×10-6m/s沿垂直于磁场同时又垂直于磁场边界的方向射入匀强磁场中,磁场的磁感应强度为B=0.17T,磁场的宽度L=10cm,如图所示.不计粒子重力.求: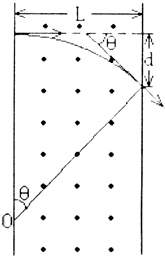 带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s沿着垂直于磁场方向又垂直磁场边界的方向进入匀强磁场,磁场的磁感应强度为B=0.17T,磁场宽度为L=10cm,求:(不计重力).
带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s沿着垂直于磁场方向又垂直磁场边界的方向进入匀强磁场,磁场的磁感应强度为B=0.17T,磁场宽度为L=10cm,求:(不计重力).