题目内容
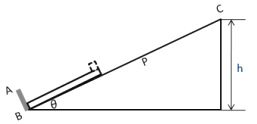
【题目】如图所示，倾角为θ=30°的光滑斜面上有固定挡板AB，斜面上B、C两点间高度差为h=4m。斜面上的P点距离C点x=5m。斜面上静止放着质量为2m的薄木板，木板下端位于挡板AB处，木板长为L=0.5m。(g=10m/s)
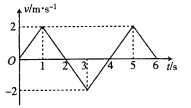
(1)若木板以某初速度沿斜面向上运动，木板上端恰能运动到C点，求初速度大小
；
(2)若给木板施加一个大小为F=1.5mg.方向沿斜面向上的拉力，要使木板上端恰能运动到C点，求拉力F作用的时间
及木板上端到达P点经历的时间
；
(3) 若给木板施加一个力F，使木板先加速后始终维持匀速，当木板上端上滑到P点时，在木板的顶端轻放一个物块，之后木板始终维持
=3m/s匀速上滑，木板和物块两者间的动摩擦因数
物块可以看成质点。问木板上端从P点到C点的过程中，物块会不会从木板上滑落? 请说明理由。
【答案】(1) 
(2) 
s或(3+
)s(3) 能
【解析】试题分析：（1）由牛顿第二定律求出木板的加速度，应用匀变速直线运动的速度位移公式求出初速度；（2）应用牛顿第二定律求出加速度，由运动学公式求出时间；（3）应用牛顿第二定律求出加速度，然后应用运动学公式求出滑块与木板的位移，再求出两者的相对位移，根据相对位移分析判断物块是否从木板上滑落.
（1）对木板，由牛顿第二定律得： 
由匀变速直线运动的速度位移公式得： 
解得： 
（2）由牛顿第二定律得：
有拉力时
，解得： 
撤去拉力后： 
，解得： 
刚撤去拉力时，木板速度： 
木板上端刚好到达C点时： 
整个过程秒表的位移： 
解得： 
木板上端第一次经过P点时： 
解得： 
木板到达C点后要沿斜面下滑，下滑过程木板上端到达P点时，有： 
解得： 
木板上端第二次到达P点需要的时间为： 
木板上端到达P点的时间为： 
或
（3）木板上端从P到C的时间： 
物块在木板上的加速度： 
物块与木板共速需要的时间： 
物块与木板达到共速时，相对斜面的位移： 
木板相对斜面的位移： 
木板与物块的相对于位移： 
物块与木板共速前已经从木板上滑落
