题目内容
（2012?黄埔区模拟）如图所示，物体A和B的质量均为m，且分别与轻绳连接跨过定滑轮，现用力拉物体B，使它沿水平面向右做匀速运动，物体B从C运动到D的过程中，物体A克服重力做功为W1，从D运动到E的过程中，物体A克服重力做功为W2．如果CD和DE的距离相等，在此过程中，绳子对物体A的拉力大小为T，下列说法中正确的是（ ）分析：由于B做匀速运动，将B的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动，得到沿绳子方向的运动速度，即物体A的速度表达式，得到A的运动规律，再根据牛顿第二定律判断绳子拉力的变化情况；根据“极限、函数的单调性”求解．
解答：解：将B的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动，如图
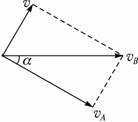解得：vA=vBcosα，α减小，则vA逐渐增大，说明A物体在竖直向上做加速运动，
由牛顿第二定律T-mg=ma，
可知绳子对A的拉力T＞mg，
物体B的速度VB恒定，前后过程中物体B位移恒定（用SB表示）．
我们假定物体B匀速运动的速度趋于零，那么根据极限的概念，在C→D→E的过程中，时间趋于无穷大．
这样的假定并不违反试题表述的物理过程．
即：VB→0，则：t1→∞、t2→∞．进一步推导得到：物体A的加速度aA→0，绳子拉力T→mg．
对物体B受力平衡分析可得：F→FTcosα，
在0≤α≤90度域内，函数cosα随α增大而减小．
根据试题表述的物理过程，在C→D→E的过程中，α递减，则F递增．
那么拉力F的平均作用力在C→D过程小于在D→E过程．
由此，根据功的定义式：W=FS，
可知：W1＜W2．
故选A．
解得：vA=vBcosα，α减小，则vA逐渐增大，说明A物体在竖直向上做加速运动，由牛顿第二定律T-mg=ma，
可知绳子对A的拉力T＞mg，
物体B的速度VB恒定，前后过程中物体B位移恒定（用SB表示）．
我们假定物体B匀速运动的速度趋于零，那么根据极限的概念，在C→D→E的过程中，时间趋于无穷大．
这样的假定并不违反试题表述的物理过程．
即：VB→0，则：t1→∞、t2→∞．进一步推导得到：物体A的加速度aA→0，绳子拉力T→mg．
对物体B受力平衡分析可得：F→FTcosα，
在0≤α≤90度域内，函数cosα随α增大而减小．
根据试题表述的物理过程，在C→D→E的过程中，α递减，则F递增．
那么拉力F的平均作用力在C→D过程小于在D→E过程．
由此，根据功的定义式：W=FS，
可知：W1＜W2．
故选A．
点评：本题关键是正确地找出物体B的合运动与分运动，然后根据运动分解的平行四边形定则，得到物体A速度的一般表达式，得出物体A处于超重状态，从而得到拉力大于重力．
练习册系列答案
阅读快车系列答案
相关题目
（2012?黄埔区模拟）如图所示，某中学科技小组制作了利用太阳能驱动小车的装置．当太阳光照射到小车上方的光电板时，光电板中产生的电流经电动机带动小车前进．小车在平直的公路上静止开始匀加速行驶，经过时间t，速度为v时功率达到额定功率，并保持不变；小车又继续前进了s距离，达到最大速度vmax．设小车的质量为m，运动过程所受阻力恒为f，则小车的额定功率为（ ）
（2012?黄埔区模拟）如图所示，质量均匀的球夹在光滑竖直墙面和光滑轻板之间，轻板可绕其L端的水平轴O自由转动．在轻板上端用竖直向上的拉力F提着轻板，使其缓慢放下，直到轻板呈水平之前，F的大小以及F对于轴O的力矩M的大小变化情况是（ ）
（2012?黄埔区模拟）如图所示的电路可用于测量电源的内阻r，电源的电动势未知．图中A 是电流表，其内阻并不很小，V为电压表，其内阻亦不很大，R是一限流电阻，阻值未知，电键S1、S2、S3都处于断开状态．